Wykres tangensa w Excelu to doskonałe narzędzie do wizualizacji funkcji trygonometrycznych. Dzięki prostym krokom możesz szybko obliczyć wartości tangensa dla różnych kątów i przedstawić je w formie graficznej. W tym artykule przedstawimy, jak wykorzystać funkcję TAN w Excelu, aby uzyskać dane, które następnie można przekształcić w wykres.
Na początku dowiesz się, jak wprowadzać kąty w odpowiednim formacie oraz jak używać funkcji TAN do obliczeń. Następnie przeprowadzimy Cię przez proces tworzenia wykresu, a także pokażemy, jak go sformatować, aby był czytelny i estetyczny. Zrozumienie wykresu tangensa jest również istotne, dlatego omówimy jego analizę w kontekście matematycznym oraz praktyczne zastosowania.
Kluczowe informacje:- Excel umożliwia obliczanie wartości tangensa za pomocą funkcji TAN.
- Wprowadzenie kątów w odpowiednim formacie (stopnie lub radiany) jest kluczowe dla dokładnych obliczeń.
- Wykres tangensa można łatwo stworzyć, organizując dane w tabeli i korzystając z opcji wstawiania wykresu w Excelu.
- Formatowanie wykresu, w tym dostosowanie osi i etykiet, poprawia jego czytelność i prezentację.
- Analiza kształtu wykresu tangensa pozwala zrozumieć jego zachowanie w różnych przedziałach kątowych.
Jak obliczyć wartości tangensa w Excelu dla wykresu
Aby obliczyć wartości tangensa w Excelu, należy skorzystać z funkcji TAN. Ta funkcja umożliwia obliczanie tangensa dla kątów wyrażonych w radianach. Wystarczy wprowadzić wartości kątów w kolumnie, a następnie w sąsiedniej kolumnie użyć formuły =TAN(A1), gdzie A1 to komórka z kątem, dla którego chcemy obliczyć tangens. Excel automatycznie obliczy wartość tangensa dla każdego z wprowadzonych kątów, co jest niezwykle przydatne w analizach matematycznych i graficznych.
Wartości kątów muszą być wprowadzane w odpowiednim formacie, aby funkcja TAN mogła poprawnie zinterpretować dane. Kąty mogą być podawane w radianach lub stopniach, w zależności od ustawień programu. W przypadku używania stopni, należy pamiętać o konwersji do radianów, ponieważ funkcje trygonometryczne w Excelu operują głównie na radianach. Można to zrobić, używając funkcji RADIANS, aby przeliczyć stopnie na radiany.
Używanie funkcji TAN do obliczeń kątowych w Excelu
Funkcja TAN w Excelu jest niezwykle prosta w użyciu. Aby obliczyć tangens, wystarczy wpisać formułę w odpowiedniej komórce. Na przykład, jeśli w komórce A1 znajduje się kąt 45°, to aby obliczyć jego tangens, w komórce B1 wpisujemy =TAN(RADIANS(A1)). Excel zwróci wartość 1, ponieważ tangens 45° wynosi 1. To narzędzie jest idealne do szybkich obliczeń, które można wykorzystać w projektach matematycznych i inżynieryjnych.
Wprowadzanie kątów w odpowiednim formacie dla obliczeń
Podczas pracy z funkcją TAN w Excelu, ważne jest, aby kąty były wprowadzane w odpowiednim formacie. Excel obsługuje zarówno stopnie, jak i radiany, ale domyślnie większość funkcji trygonometrycznych, w tym TAN, wymaga użycia radianów. Można łatwo konwertować stopnie na radiany, korzystając z funkcji RADIANS. Na przykład, aby przeliczyć 90° na radiany, można użyć formuły =RADIANS(90), co zwróci wartość π/2. Upewnij się, że zawsze wprowadzasz kąty w odpowiednim formacie, aby obliczenia były poprawne.
Jak stworzyć wykres tangensa w Excelu krok po kroku
Aby stworzyć wykres tangensa w Excelu, należy najpierw obliczyć wartości tangensa dla wybranych kątów. Proces ten obejmuje wprowadzenie odpowiednich danych do arkusza kalkulacyjnego, a następnie wykorzystanie funkcji w Excelu, aby uzyskać pożądane wyniki. W dalszej części omówimy szczegółowo, jak zorganizować dane oraz jak wstawić wykres na podstawie tych obliczeń.
Na początku musisz przygotować dane, które będą służyły jako podstawa do wykresu. Wprowadź kąty w jednej kolumnie, a w sąsiedniej kolumnie oblicz ich tangens za pomocą funkcji TAN. Po zebraniu danych, możesz przejść do etapu tworzenia wykresu. Wybierz odpowiedni typ wykresu, aby najlepiej zobrazować funkcję tangensa.
Tworzenie danych do wykresu tangensa w Excelu
Organizacja danych jest kluczowa dla skutecznego stworzenia wykresu. Zacznij od wprowadzenia kątów w kolumnie A, zaczynając od komórki A1. Następnie w kolumnie B, w komórce B1, wpisz formułę =TAN(RADIANS(A1)), aby obliczyć tangens dla kąta w stopniach. Przeciągnij formułę w dół, aby obliczyć tangens dla wszystkich wprowadzonych kątów. Upewnij się, że masz odpowiednią ilość danych, aby wykres był czytelny i informacyjny.
| Kąt (stopnie) | Tangens |
| 0 | 0 |
| 30 | 0.5774 |
| 45 | 1 |
| 60 | 1.7321 |
| 90 | #DZIEL/0! |
Wstawianie wykresu na podstawie obliczonych wartości
Gdy masz już przygotowane dane, czas na wstawienie wykresu. Zaznacz dane w kolumnach A i B, a następnie przejdź do zakładki Wstaw w Excelu. Wybierz typ wykresu, który najlepiej pasuje do Twoich danych; dla funkcji tangensa idealny będzie wykres liniowy. Po wybraniu wykresu, Excel automatycznie wygeneruje wizualizację na podstawie obliczonych wartości tangensa.
Możesz dostosować wykres, aby lepiej odzwierciedlał Twoje dane. Zmień tytuł wykresu, dodaj etykiety osi oraz dostosuj kolory, aby wykres był bardziej czytelny. Pamiętaj, że dobrze skonstruowany wykres ułatwi analizę i zrozumienie funkcji tangensa.
Czytaj więcej: Jak uzasadnić odroczenie obowiązku szkolnego? Porady dla rodziców
Jak formatować wykres tangensa dla lepszej czytelności
Formatowanie wykresu tangensa jest kluczowe dla jego czytelności i zrozumienia. Dobrze sformatowany wykres nie tylko prezentuje dane w estetyczny sposób, ale również ułatwia interpretację wyników. W tej sekcji omówimy kilka istotnych aspektów, które warto wziąć pod uwagę, aby poprawić wygląd i funkcjonalność wykresu.
Jednym z pierwszych kroków w formatowaniu wykresu jest dostosowanie osi i etykiet. Upewnij się, że osie są odpowiednio opisane, aby widzowie mogli łatwo zrozumieć, co przedstawiają. Możesz również zmienić skale osi, aby lepiej odzwierciedlały zakres danych. Dostosowanie kolorów i stylów linii może również pomóc w wyróżnieniu ważnych informacji.
Dostosowanie osi i etykiet w wykresie tangensa
W Excelu można łatwo dostosować osie i etykiety wykresu, co znacząco wpływa na jego czytelność. Aby to zrobić, kliknij prawym przyciskiem myszy na oś, którą chcesz edytować, i wybierz opcję Formatuj oś. Możesz zmienić zakres wartości, co pozwoli lepiej dopasować oś do danych. Dodatkowo, warto dodać etykiety do osi, aby jasno wskazywały, jakie wartości są przedstawiane.
Zmiana stylu wykresu dla lepszej prezentacji danych
W Excelu dostępnych jest wiele stylów wykresów, które można wykorzystać do poprawy wizualizacji danych. Wybierając styl, warto zwrócić uwagę na to, jak różne kolory i wzory linii wpływają na interpretację wykresu. Możesz na przykład użyć stylu z większymi punktami danych, aby wyróżnić kluczowe wartości. Użycie kontrastujących kolorów może również pomóc w podkreśleniu różnic między różnymi seriami danych.
Jak interpretować wykres tangensa w kontekście matematyki
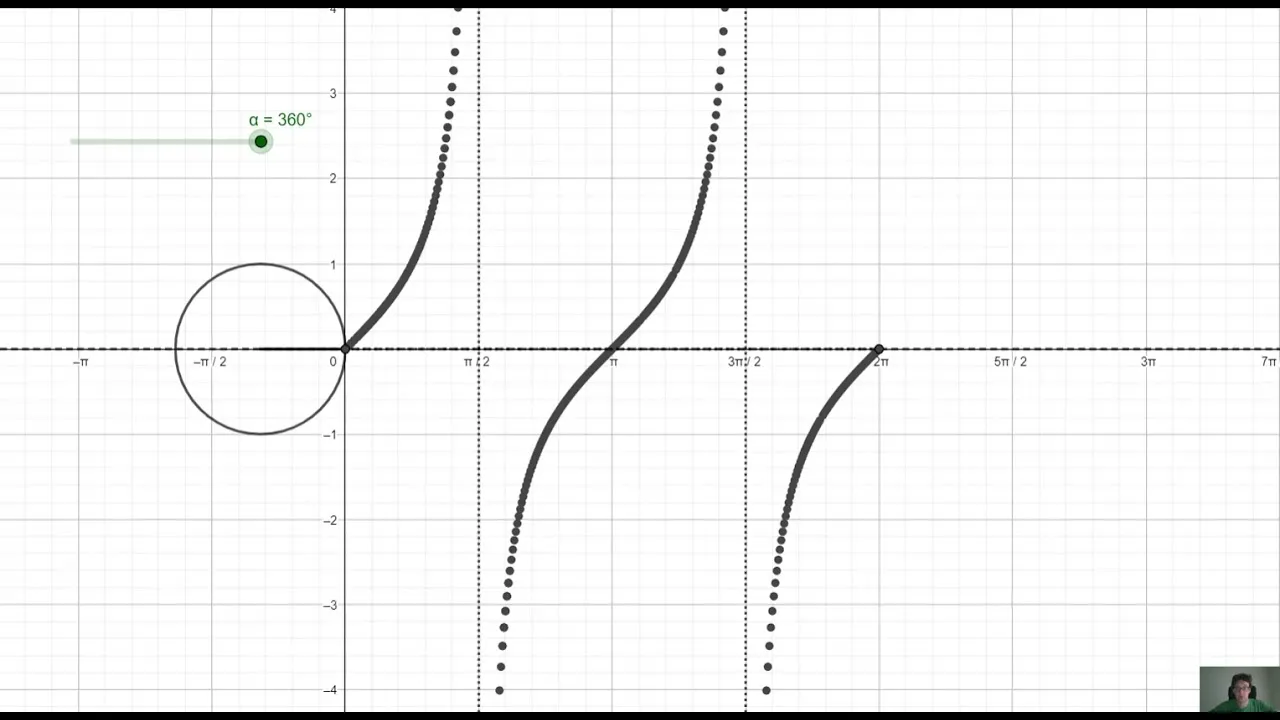
Interpretacja wykresu tangensa jest kluczowym elementem analizy funkcji trygonometrycznych. Wykres ten pokazuje, jak wartości tangensa zmieniają się w zależności od kąta. Zrozumienie kształtu wykresu oraz jego zachowania w różnych przedziałach kątowych pozwala lepiej zrozumieć właściwości funkcji tangens. W tej sekcji omówimy, jak analizować wykres tangensa, zwracając uwagę na jego charakterystyczne cechy.
Warto zauważyć, że funkcja tangensa ma okresowość i asymptoty. Wykres tangensa ma charakterystyczne punkty, w których funkcja dąży do nieskończoności, co ma miejsce w punktach, gdzie kąt wynosi 90° + n*180°, gdzie n jest liczbą całkowitą. W takich miejscach wykres "wystrzela" w górę lub w dół, co jest istotne przy analizie zachowania funkcji.
Analiza kształtu wykresu tangensa w różnych przedziałach kątowych
W różnych przedziałach kątowych wykres tangensa zachowuje się w specyficzny sposób. Na przykład, w przedziale od 0° do 90°, wartości tangensa rosną od 0 do nieskończoności. W przedziale od 90° do 180°, funkcja maleje od nieskończoności do 0. Te zmiany są kluczowe dla zrozumienia, jak funkcja tangens reaguje na zmiany kąta i jak można je wykorzystać w praktyce.
Warto również zauważyć, że w przedziałach od 180° do 270° oraz od 270° do 360° wykres tangensa znowu przyjmuje wartości od 0 do nieskończoności i od nieskończoności do 0, co powtarza się w cyklu. Te właściwości sprawiają, że funkcja tangens jest użyteczna w wielu zastosowaniach matematycznych, w tym w analizie kątów w geometrii i fisyce.
Przykłady zastosowania wykresu tangensa w praktyce matematycznej
Wykres tangensa ma wiele praktycznych zastosowań w matematyce oraz naukach ścisłych. Na przykład, w trigonometrii jest używany do analizy kątów w różnych kontekstach, takich jak obliczanie wysokości obiektów czy odległości w terenie. Dzięki wykresowi tangensa można łatwo zrozumieć, jak zmieniają się wartości funkcji w zależności od kąta, co jest kluczowe w wielu obliczeniach inżynieryjnych.
Innym przykładem zastosowania wykresu tangensa jest w fizyce, gdzie funkcja tangens jest używana do analizy ruchu obrotowego oraz w obliczeniach związanych z kinematyką. Na przykład, w przypadku analizy trajektorii obiektów rzuconych pod kątem, wykres tangensa może pomóc w wizualizacji i zrozumieniu, jak zmienia się kąt i prędkość w czasie. Wykresy te są również przydatne w optyce, gdzie mogą ilustrować różne właściwości światła.
Jak wykorzystać wykres tangensa w programowaniu i symulacjach
Wykres tangensa nie tylko pomaga w analizie kątów w matematyce, ale również znajduje zastosowanie w programowaniu i symulacjach komputerowych. Dzięki funkcji tangens można modelować zjawiska fizyczne, takie jak ruch obrotowy czy fale, co jest szczególnie przydatne w grach komputerowych oraz symulacjach inżynieryjnych. Na przykład, w silnikach gier, funkcja tangens jest używana do obliczania kątów widzenia kamery, co pozwala na realistyczne odwzorowanie ruchu obiektów w przestrzeni 3D.
Dodatkowo, w kontekście uczenia maszynowego i sztucznej inteligencji, wykres tangensa może być użyty do analizy danych oraz optymalizacji algorytmów. W przypadku analizy danych, zrozumienie, jak wartości tangensa zmieniają się w różnych warunkach, pozwala na lepsze przewidywanie wyników i podejmowanie decyzji na podstawie danych. Użycie wykresów tangensa w tych dziedzinach otwiera nowe możliwości dla programistów i analityków, umożliwiając tworzenie bardziej zaawansowanych modeli i symulacji.
