Wyrażenia algebraiczne są podstawowym elementem matematyki, który uczniowie klasy 7 muszą zrozumieć, aby skutecznie poruszać się w świecie liczb i równań. Składają się one z liczb, liter, znaków działań i nawiasów, co pozwala na wyrażenie różnych zależności i sytuacji matematycznych. W tej lekcji przyjrzymy się, jak zrozumieć te wyrażenia, jakie są ich elementy oraz jak je upraszczać.
W kolejnych częściach artykułu przedstawimy proste przykłady wyrażeń algebraicznych i wyjaśnimy, jak tworzyć je na podstawie codziennych sytuacji. Dzięki temu uczniowie będą mogli lepiej zrozumieć, jak zastosować te pojęcia w praktyce. Na koniec zaproponujemy ćwiczenia, które pomogą w utrwaleniu zdobytej wiedzy. Kluczowe informacje:- Wyrażenia algebraiczne składają się z liczb, zmiennych i operatorów.
- Różnica między wyrażeniem a równaniem polega na tym, że równanie zawiera znak równości.
- Uproszczenie wyrażeń algebraicznych można osiągnąć poprzez dodawanie, odejmowanie, mnożenie i dzielenie.
- Przykłady wyrażeń algebraicznych można znaleźć w codziennych sytuacjach, co ułatwia ich zrozumienie.
- Praktyczne ćwiczenia są kluczowe dla utrwalenia wiedzy o wyrażeniach algebraicznych.
Zrozumienie wyrażeń algebraicznych poprzez definicje i przykłady
Wyrażenia algebraiczne to fundamentalny element matematyki, który składa się z liczb, liter, znaków działań i nawiasów. Służą one do przedstawiania różnych zależności i sytuacji matematycznych. W kontekście klasy 7, zrozumienie tych wyrażeń jest kluczowe, ponieważ stanowią one podstawę do nauki bardziej złożonych zagadnień matematycznych. Uczniowie powinni poznać różne składniki wyrażeń algebraicznych, aby skutecznie je stosować w praktyce.
Podstawowe elementy wyrażeń algebraicznych to zmienne, stałe i współczynniki. Zmienne to symbole, które reprezentują nieznane wartości, najczęściej oznaczane literami, takimi jak x czy y. Stałe to liczby, które nie zmieniają swojej wartości, na przykład 5 lub 10. Współczynniki to liczby, które mnożą zmienne, na przykład w wyrażeniu 3x, liczba 3 jest współczynnikiem. Zrozumienie tych elementów jest kluczowe dla dalszej nauki o wyrażeniach algebraicznych i ich zastosowaniach.
Co to są wyrażenia algebraiczne i ich elementy?
Wyrażenia algebraiczne to kombinacje liczb, zmiennych oraz operatorów matematycznych, które pozwalają na tworzenie równań i analizowanie relacji między różnymi wartościami. Elementy wyrażenia algebraicznego obejmują termy, współczynniki i stałe. Term to jednostka wyrażenia, która może być liczbą, zmienną lub ich kombinacją. Na przykład w wyrażeniu 2x + 3, mamy dwa termy: 2x i 3. Współczynniki to liczby, które mnożą zmienne w wyrażeniu, natomiast stałe to liczby, które nie zmieniają się.Jakie są różnice między wyrażeniami a równaniami?
Wyrażenia algebraiczne i równania to dwa podstawowe pojęcia w matematyce, które często są mylone. Wyrażenie algebraiczne to kombinacja liczb, zmiennych oraz operatorów matematycznych, która nie zawiera znaku równości. Na przykład, wyrażenie 3x + 5 jest wyrażeniem algebraicznym, które przedstawia sumę zmiennej x pomnożonej przez 3 oraz liczby 5. Z kolei równanie to stwierdzenie, które twierdzi, że dwie wartości są sobie równe i zawiera znak równości. Przykładem równania może być 3x + 5 = 11, które wskazuje, że wyrażenie po lewej stronie jest równe 11.Ważne jest, aby zrozumieć, że wyrażenia algebraiczne mogą być częścią równań, ale nie każde wyrażenie jest równaniem. Równania są używane do rozwiązywania problemów, w których musimy znaleźć wartość zmiennej, podczas gdy wyrażenia służą do przedstawiania wartości w bardziej ogólny sposób. Ta różnica jest kluczowa dla uczniów klasy 7, którzy uczą się, jak zrozumieć i stosować te pojęcia w praktyce.
Proste przykłady wyrażeń algebraicznych dla uczniów
W tej sekcji przyjrzymy się prostym przykładom wyrażeń algebraicznych, które są istotne dla uczniów klasy 7. Zrozumienie tych przykładów pomoże uczniom lepiej poruszać się w świecie matematyki. Wyrażenia algebraiczne mogą być używane do przedstawiania różnych sytuacji, co czyni je bardzo przydatnymi w codziennym życiu. Na przykład, wyrażenie 2x + 3 może reprezentować całkowity koszt zakupu dwóch przedmiotów, z których każdy kosztuje x złotych oraz dodatkowych 3 złote za opakowanie.
Innym przykładem może być wyrażenie 4y - 7, które może opisywać sytuację, w której mamy 4 razy więcej jabłek niż y, a następnie odejmujemy 7 jabłek. Takie wyrażenia są nie tylko użyteczne, ale także pomagają uczniom zrozumieć, jak można modelować rzeczywistość za pomocą matematyki. Uczniowie powinni ćwiczyć tworzenie i analizowanie takich wyrażeń, aby stały się one dla nich bardziej intuicyjne i zrozumiałe.
Przykłady wyrażeń algebraicznych z użyciem zmiennych
Wyrażenia algebraiczne z użyciem zmiennych są kluczowym elementem w nauce matematyki. Przykłady takich wyrażeń pomagają uczniom zrozumieć, jak zmienne mogą reprezentować różne wartości. Na przykład, wyrażenie 5x + 2 pokazuje, że mamy pięć razy wartość zmiennej x oraz dodatkowe 2. Inny przykład to 3y - 4, gdzie 3y oznacza, że mamy trzy razy wartość zmiennej y, a następnie odejmujemy 4. Takie wyrażenia są proste, ale bardzo użyteczne w codziennych zastosowaniach matematycznych.
- 2a + 3: To wyrażenie oznacza, że mamy dwa razy wartość zmiennej a, a następnie dodajemy 3.
- 4b - 7: Tutaj mamy cztery razy wartość zmiennej b, z której odejmujemy 7.
- 6c + 1: W tym przypadku mamy sześć razy wartość zmiennej c oraz dodajemy 1.
- 7d: To wyrażenie pokazuje, że mamy siedem razy wartość zmiennej d, bez dodatkowych operacji.
- 8e - 10: W tym wyrażeniu mamy osiem razy wartość zmiennej e, z której odejmujemy 10.
- 9f + 12: To wyrażenie oznacza, że mamy dziewięć razy wartość zmiennej f oraz dodajemy 12.
Jak tworzyć wyrażenia algebraiczne z codziennych sytuacji?
Tworzenie wyrażeń algebraicznych z codziennych sytuacji to świetny sposób na zrozumienie, jak matematyka odnosi się do rzeczywistości. Uczniowie mogą zacząć od zidentyfikowania sytuacji, które można opisać za pomocą zmiennych. Na przykład, jeśli chcemy obliczyć całkowity koszt zakupu x jabłek, które kosztują 2 złote każde, możemy stworzyć wyrażenie 2x. Innym przykładem może być sytuacja, w której mamy y złotych, a chcemy kupić 3 zeszyty po 4 złote każdy. Wyrażenie 4 * 3 - y pomoże nam obliczyć, ile pieniędzy nam zostanie po zakupie zeszytów. Dzięki tym przykładom uczniowie mogą lepiej zrozumieć, jak wyrażenia algebraiczne są używane w codziennym życiu.
Czytaj więcej: Wypalenie zawodowe nauczycieli: przyczyny, objawy i rozwiązania
Krok po kroku: jak upraszczać wyrażenia algebraiczne?

Upraszczanie wyrażeń algebraicznych to ważna umiejętność, którą uczniowie klasy 7 muszą opanować. Proces ten polega na redukcji wyrażenia do prostszej formy, co ułatwia dalsze obliczenia i analizy. Aby uprościć wyrażenie, należy stosować różne zasady i techniki, takie jak łączenie podobnych terminów oraz stosowanie właściwych reguł arytmetycznych. Na przykład w wyrażeniu 3x + 2x, można połączyć podobne terminy, co daje 5x.
Innym ważnym krokiem w upraszczaniu wyrażeń jest używanie nawiasów. Kiedy mamy wyrażenie takie jak 2(x + 3), najpierw mnożymy 2 przez każdy składnik w nawiasie, co daje 2x + 6. Uczniowie powinni ćwiczyć te techniki, aby stały się one dla nich naturalne. Dzięki temu, będą w stanie szybko i efektywnie upraszczać różne wyrażenia algebraiczne, co jest kluczowe w dalszej nauce matematyki.
Zasady upraszczania: dodawanie i odejmowanie wyrażeń
Dodawanie i odejmowanie wyrażeń algebraicznych opiera się na łączeniu podobnych terminów. Aby dodać lub odjąć wyrażenia, należy upewnić się, że terminy są podobne, co oznacza, że mają te same zmienne i potęgi. Na przykład, w wyrażeniu 4x + 3x, możemy dodać współczynniki, co daje 7x. W przypadku odejmowania, na przykład w wyrażeniu 5y - 2y, również łączymy podobne terminy, co daje 3y.
Ważne jest, aby pamiętać, że podczas dodawania lub odejmowania wyrażeń, nie możemy łączyć terminów, które są różne. Na przykład, w wyrażeniu 2x + 3y, nie możemy połączyć 2x z 3y, ponieważ mają różne zmienne. Uczniowie powinni ćwiczyć te zasady, aby stały się one dla nich zrozumiałe i intuicyjne, co pomoże w dalszym rozwoju umiejętności matematycznych.
Mnożenie i dzielenie w wyrażeniach algebraicznych
Mnożenie i dzielenie wyrażeń algebraicznych to kluczowe umiejętności, które uczniowie klasy 7 muszą opanować. Mnożenie polega na łączeniu wyrażeń, co wymaga zastosowania reguł dotyczących współczynników i zmiennych. Na przykład, w przypadku wyrażenia 2x * 3y, mnożymy liczby (2 i 3), a następnie łączymy zmienne, co daje 6xy. Warto pamiętać, że przy mnożeniu zmiennych, ich kolejność nie ma znaczenia, więc 3y * 2x również daje 6xy.
Podobnie, dzielenie wyrażeń algebraicznych polega na podzieleniu współczynników i odpowiednich zmiennych. Na przykład, w wyrażeniu 6x / 2, dzielimy 6 przez 2, co daje 3x. W przypadku dzielenia zmiennych, takich jak x^2 / x, możemy zastosować zasady potęg, co daje x^(2-1) = x. Uczniowie powinni ćwiczyć te zasady, aby stały się one dla nich naturalne i ułatwiały rozwiązywanie bardziej złożonych problemów matematycznych.
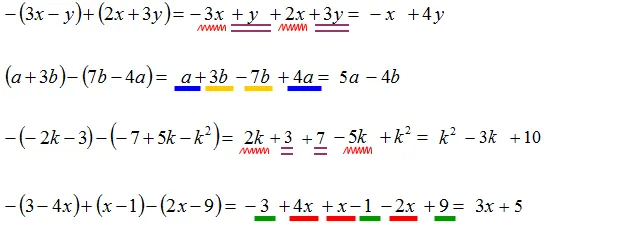
Ćwiczenia praktyczne dla lepszego zrozumienia tematu
Praktyczne ćwiczenia są kluczowe dla utrwalenia umiejętności związanych z wyrażeniami algebraicznymi. Uczniowie mogą zacząć od prostych zadań, takich jak mnożenie i dzielenie wyrażeń, a następnie przechodzić do bardziej złożonych problemów, które wymagają zastosowania różnych technik. Na przykład, mogą rozwiązywać zadania, w których muszą uprościć wyrażenie, takie jak 4x * 5y, lub podzielić 10xy przez 2x. Regularne ćwiczenie pomoże im zrozumieć zasady i techniki, które są niezbędne do skutecznego rozwiązywania problemów matematycznych.
Ważne jest również, aby uczniowie analizowali swoje wyniki i uczyli się na błędach. Dzięki temu będą mogli poprawić swoje umiejętności i zrozumienie wyrażeń algebraicznych. Na przykład, po rozwiązaniu zadania, warto sprawdzić, czy wyniki są logiczne i zgodne z zasadami matematycznymi. Takie podejście pozwoli na skuteczniejsze przyswajanie wiedzy i lepsze przygotowanie do przyszłych wyzwań w matematyce.
Przykładowe zadania do samodzielnego rozwiązania
Aby pomóc uczniom w praktycznym zastosowaniu zdobytej wiedzy, przygotowano zestaw zadań do samodzielnego rozwiązania. Uczniowie powinni spróbować rozwiązać poniższe problemy, które obejmują różne typy wyrażeń algebraicznych. Przykłady zadań mogą obejmować mnożenie, dzielenie oraz uproszczenie wyrażeń, co pozwoli na lepsze zrozumienie tematu.
| Zadanie | Opis |
| 1 | Oblicz 3x * 4y |
| 2 | Uprość wyrażenie 5a + 3a |
| 3 | Oblicz 12xy / 4x |
| 4 | Uprość 2x + 5 - 3x + 4 |
| 5 | Oblicz 6a * 2b |
Jak wykorzystać wyniki ćwiczeń do poprawy umiejętności?
Analizowanie wyników ćwiczeń jest kluczowym krokiem w procesie nauki. Uczniowie powinni regularnie przeglądać swoje odpowiedzi i zastanawiać się, co poszło dobrze, a co można poprawić. Na przykład, jeśli uczniowie popełniają błędy w mnożeniu lub dzieleniu, mogą skupić się na tych konkretnych obszarach, aby lepiej zrozumieć zasady. Ponadto, warto korzystać z dodatkowych materiałów, takich jak ćwiczenia online lub podręczniki, które oferują różnorodne zadania i wyjaśnienia.
Ważne jest, aby uczniowie nie tylko uczyli się na błędach, ale także świętowali swoje sukcesy. Rozwiązywanie zadań, które wcześniej sprawiały trudności, i osiąganie pozytywnych wyników wzmacnia pewność siebie w matematyce. Regularne ćwiczenie oraz refleksja nad wynikami pomogą w długoterminowym zrozumieniu wyrażeń algebraicznych i ich zastosowania w praktyce.
Jak wykorzystać wyrażenia algebraiczne w codziennym życiu?
Wyrażenia algebraiczne mają zastosowanie nie tylko w matematyce szkolnej, ale również w codziennym życiu, co czyni je niezwykle praktycznymi. Na przykład, podczas planowania budżetu domowego, można użyć wyrażeń algebraicznych do obliczenia wydatków. Jeśli mamy stałą kwotę pieniędzy, którą chcemy wydać na zakupy, możemy stworzyć wyrażenie, które uwzględnia ceny różnych produktów. Na przykład, jeśli x to cena jednego produktu, a y to cena drugiego, nasze wydatki mogą być opisane jako 2x + 3y. Dzięki temu możemy łatwo zobaczyć, ile wydamy na zakupy, co pozwoli nam lepiej zarządzać finansami.
Innym praktycznym zastosowaniem wyrażeń algebraicznych jest ich wykorzystanie w różnych zawodach, takich jak inżynieria, architektura czy nauki przyrodnicze. W tych dziedzinach wyrażenia algebraiczne służą do modelowania różnych zjawisk i rozwiązywania problemów. Na przykład, inżynierowie mogą używać wyrażeń algebraicznych do obliczenia sił działających na konstrukcje, co jest kluczowe dla zapewnienia ich stabilności. W ten sposób uczniowie, ucząc się wyrażeń algebraicznych, rozwijają umiejętności, które będą im przydatne w przyszłości, niezależnie od wybranej ścieżki kariery.





