Wzór na pole trójkąta jest kluczowym elementem w geometrii, który pozwala na obliczenie powierzchni tego kształtu. Podstawową formułą jest połowa iloczynu długości podstawy oraz wysokości opuszczonej na tę podstawę. Można to zapisać jako P = 1/2 * a * h, gdzie a to długość podstawy, a h to wysokość. Ta prosta formuła jest niezwykle przydatna w wielu sytuacjach, zarówno w edukacji, jak i w praktycznych zastosowaniach.
Jednakże, istnieją także inne metody obliczania pola trójkąta, które mogą być użyteczne, gdy dostępne są różne dane. Na przykład, jeśli znamy długości dwóch boków oraz kąt między nimi, możemy użyć wzoru z wykorzystaniem sinusa: P = 1/2 * a * b * sin(γ). W tym artykule przyjrzymy się tym różnym metodom oraz przedstawimy praktyczne przykłady, które pomogą lepiej zrozumieć temat.
Kluczowe informacje:- Podstawowy wzór na pole trójkąta to P = 1/2 * a * h, gdzie a to długość podstawy, a h to wysokość.
- Inna metoda obliczania pola trójkąta to wykorzystanie długości boków i kąta: P = 1/2 * a * b * sin(γ).
- W przypadku trójkąta prostokątnego, wzór pozostaje taki sam, ponieważ można bezpośrednio użyć podstawy i wysokości.
- Trójkąt równoboczny ma swoje unikalne właściwości, a jego pole można obliczyć na podstawie długości boku.
- Przykłady obliczeń pomogą zobrazować zastosowanie wzorów w praktyce.
Wzór na pole trójkąta – podstawowe informacje i zastosowanie
Wzór na pole trójkąta jest kluczowym elementem w geometrii. Podstawowym wzorem jest P = 1/2 * a * h, gdzie a oznacza długość podstawy, a h to wysokość trójkąta. Ta formuła pozwala na szybkie obliczenie powierzchni trójkąta, co jest przydatne w wielu dziedzinach, od edukacji po inżynierię.
Obliczanie pola trójkąta za pomocą tego wzoru jest proste i intuicyjne. Wystarczy zmierzyć długość podstawy oraz wysokość, a następnie zastosować wzór. Dzięki temu można z łatwością określić powierzchnię trójkąta w różnych sytuacjach, takich jak projektowanie, budownictwo czy nawet w codziennych zadaniach.
Jak obliczyć pole trójkąta przy użyciu podstawy i wysokości
Aby obliczyć pole trójkąta przy użyciu podstawy i wysokości, należy najpierw zidentyfikować odpowiednie wymiary. Wzór, który należy zastosować, to P = 1/2 * a * h. Ważne jest, aby wysokość była opuszczona na podstawę, co oznacza, że musi być prostopadła do niej. Dzięki temu obliczenia będą dokładne.
Na przykład, jeśli mamy trójkąt o podstawie długości 10 cm i wysokości 5 cm, obliczenie pola wygląda następująco: P = 1/2 * 10 * 5 = 25 cm². W ten sposób możemy szybko uzyskać wynik, który jest niezbędny w wielu zastosowaniach praktycznych.
- Zidentyfikuj długość podstawy trójkąta.
- Zmierz wysokość, która jest prostopadła do podstawy.
- Podstaw wartości do wzoru P = 1/2 * a * h.
- Oblicz pole trójkąta.
Inne metody obliczania pola trójkąta z wykorzystaniem boków
Obliczanie pola trójkąta nie ogranicza się tylko do metody podstawy i wysokości. Istnieją alternatywne wzory, które można zastosować, gdy znamy długości boków trójkąta oraz kąt między nimi. Jednym z najpopularniejszych wzorów jest wzór sinusowy, który pozwala na obliczenie pola trójkąta na podstawie dwóch boków i kąta, który je łączy. Wzór ten ma postać: P = 1/2 * a * b * sin(γ), gdzie a i b to długości boków, a γ to kąt między nimi.
Na przykład, jeśli mamy trójkąt, w którym długości boków wynoszą 8 cm i 6 cm, a kąt między nimi to 30 stopni, możemy obliczyć pole trójkąta w następujący sposób: P = 1/2 * 8 * 6 * sin(30°). Ponieważ sin(30°) = 0.5, obliczenia wyglądają następująco: P = 1/2 * 8 * 6 * 0.5 = 12 cm². Taka metoda jest szczególnie przydatna w przypadku trójkątów, w których wysokość nie jest łatwa do zmierzenia.
| Zmienne | Wartości |
| Długość boku a | 8 cm |
| Długość boku b | 6 cm |
| Kąt γ | 30° |
| Pole trójkąta | 12 cm² |
Obliczanie pola trójkąta prostokątnego – krok po kroku
Obliczanie pola trójkąta prostokątnego jest bardzo proste, ponieważ możemy wykorzystać znany wzór: P = 1/2 * a * h. W tym przypadku a to długość podstawy, a h to wysokość, która jest zawsze prostopadła do podstawy. Trójkąt prostokątny ma jedną kąt prosty, co ułatwia pomiar tych dwóch wymiarów i bezpośrednie zastosowanie wzoru.Przykładowo, jeśli mamy trójkąt prostokątny, w którym długość podstawy wynosi 6 cm, a wysokość 4 cm, obliczenie pola będzie wyglądać następująco: P = 1/2 * 6 * 4 = 12 cm². To oznacza, że pole tego trójkąta wynosi 12 cm², co jest przydatne w różnych zastosowaniach, od projektowania po obliczenia w codziennym życiu.
Jak znaleźć pole trójkąta równobocznego i jego właściwości
Trójkąt równoboczny to taki, w którym wszystkie boki są równej długości, a wszystkie kąty mają po 60 stopni. Aby obliczyć pole trójkąta równobocznego, możemy skorzystać z wzoru: P = (a² * √3) / 4, gdzie a to długość boku. Ta formuła wykorzystuje unikalne właściwości trójkątów równobocznych, co czyni ją efektywną w obliczeniach.
Na przykład, jeśli długość boku trójkąta równobocznego wynosi 5 cm, obliczenie pola będzie wyglądać tak: P = (5² * √3) / 4 = (25 * √3) / 4 ≈ 10,83 cm². Taki wynik pokazuje, jak łatwo można obliczyć pole trójkąta równobocznego, korzystając z jego specyficznych właściwości.
| Typ trójkąta | Wzór na pole | Właściwości |
| Trójkąt prostokątny | P = 1/2 * a * h | Ma jeden kąt prosty |
| Trójkąt równoboczny | P = (a² * √3) / 4 | Wszystkie boki równej długości |
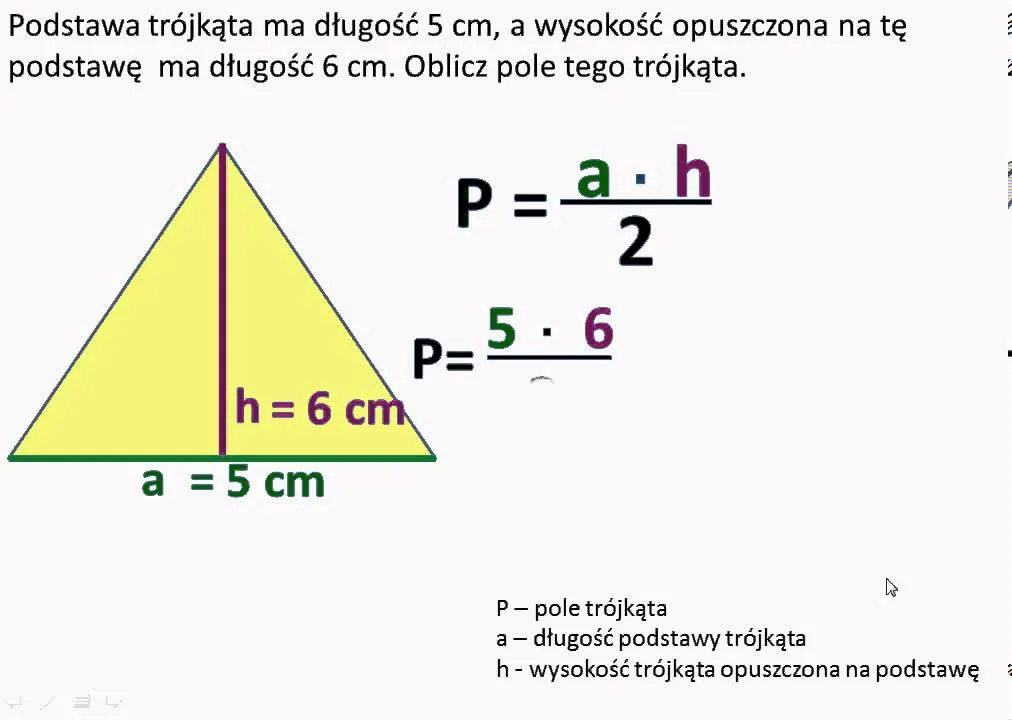
Przykłady obliczeń pola trójkąta – praktyczne zastosowanie wzorów
Praktyczne przykłady obliczeń pola trójkąta są niezwykle ważne, ponieważ pokazują, jak zastosować teoretyczne wzory w rzeczywistych sytuacjach. Dzięki tym przykładom można lepiej zrozumieć, jak różne metody obliczania pola trójkąta działają w praktyce. Poniżej przedstawiamy dwa różne scenariusze, które ilustrują zastosowanie wzorów w obliczeniach.Przykłady z wykorzystaniem podstawy i wysokości trójkąta
Rozważmy trójkąt o podstawie długości 8 cm i wysokości 5 cm. Aby obliczyć pole, stosujemy wzór: P = 1/2 * a * h. Podstawiając wartości, otrzymujemy: P = 1/2 * 8 * 5 = 20 cm². To oznacza, że pole tego trójkąta wynosi 20 cm², co jest przydatne w wielu kontekstach, takich jak projektowanie czy obliczenia w budownictwie.
W innym przykładzie rozważmy trójkąt, którego podstawa ma długość 10 cm, a wysokość wynosi 4 cm. Obliczamy pole w następujący sposób: P = 1/2 * 10 * 4 = 20 cm². W tym przypadku również uzyskujemy pole 20 cm², co pokazuje, że różne kombinacje podstawy i wysokości mogą prowadzić do tego samego wyniku.
Obliczenia pola trójkąta przy znanych bokach i kącie
W przypadku trójkąta, w którym znamy długości dwóch boków oraz kąt między nimi, możemy wykorzystać wzór sinusowy. Na przykład, jeśli długości boków wynoszą 7 cm i 9 cm, a kąt między nimi to 45 stopni, obliczamy pole w następujący sposób: P = 1/2 * a * b * sin(γ). Podstawiając wartości, otrzymujemy: P = 1/2 * 7 * 9 * sin(45°). Ponieważ sin(45°) ≈ 0.707, obliczenia wyglądają następująco: P ≈ 1/2 * 7 * 9 * 0.707 ≈ 22.12 cm².
W innym scenariuszu, dla boków długości 6 cm i 8 cm oraz kąta 30 stopni, obliczamy pole: P = 1/2 * 6 * 8 * sin(30°). Znamy wartość sin(30°) = 0.5, więc: P = 1/2 * 6 * 8 * 0.5 = 12 cm². To pokazuje, jak różne metody obliczania pola trójkąta mogą być zastosowane w praktyce.| Scenariusz | Wzór | Wynik |
| Trójkąt z podstawą i wysokością | P = 1/2 * a * h | 20 cm² |
| Trójkąt z bokami i kątem | P = 1/2 * a * b * sin(γ) | 22.12 cm² |
Przykłady z wykorzystaniem podstawy i wysokości trójkąta
Rozważmy trójkąt o podstawie długości 12 cm i wysokości 5 cm. Aby obliczyć pole tego trójkąta, zastosujemy wzór: P = 1/2 * a * h. Podstawiając wartości, otrzymujemy: P = 1/2 * 12 * 5 = 30 cm². To oznacza, że pole tego trójkąta wynosi 30 cm², co jest przydatne w różnych kontekstach, takich jak projektowanie graficzne czy budownictwo.
W innym przykładzie, weźmy trójkąt, którego podstawa ma długość 9 cm, a wysokość wynosi 6 cm. Obliczamy pole w następujący sposób: P = 1/2 * 9 * 6 = 27 cm². Taki wynik pokazuje, że różne kombinacje podstawy i wysokości mogą prowadzić do różnych wartości pola, co jest istotne w praktycznych zastosowaniach.
Obliczenia pola trójkąta przy znanych bokach i kącie
W przypadku trójkąta, w którym znamy długości dwóch boków oraz kąt między nimi, możemy wykorzystać wzór sinusowy. Na przykład, załóżmy, że długości boków wynoszą 10 cm i 7 cm, a kąt między nimi to 60 stopni. Obliczamy pole w następujący sposób: P = 1/2 * a * b * sin(γ). Podstawiając wartości, otrzymujemy: P = 1/2 * 10 * 7 * sin(60°). Ponieważ sin(60°) ≈ 0.866, obliczenia wyglądają tak: P ≈ 1/2 * 10 * 7 * 0.866 ≈ 30.41 cm².
W innym scenariuszu, dla boków długości 5 cm i 8 cm oraz kąta 45 stopni, obliczamy pole: P = 1/2 * 5 * 8 * sin(45°). Znamy wartość sin(45°) ≈ 0.707, więc: P ≈ 1/2 * 5 * 8 * 0.707 ≈ 14.14 cm². To pokazuje, jak różne metody obliczania pola trójkąta mogą być zastosowane w praktyce.
| Scenariusz | Wzór | Wynik |
| Trójkąt z podstawą i wysokością | P = 1/2 * a * h | 30 cm² |
| Trójkąt z bokami i kątem | P = 1/2 * a * b * sin(γ) | 30.41 cm² |
Czytaj więcej: Zmiana szkoły w trakcie roku - sprawna procedura z pozytywnym skutkiem
Jak wykorzystać wzory na pole trójkąta w projektowaniu
Wzory na pole trójkąta mogą być niezwykle przydatne nie tylko w matematyce, ale także w projektowaniu i architekturze. Na przykład, podczas planowania przestrzeni, architekci często muszą obliczać powierzchnie różnych kształtów, w tym trójkątów, aby zoptymalizować wykorzystanie materiałów i przestrzeni. Znając wzory na pole trójkąta, mogą szybko i efektywnie oszacować ilość potrzebnych materiałów, co przekłada się na oszczędności finansowe i czasowe.
Dodatkowo, w kontekście inżynierii i budownictwa, znajomość tych wzorów jest kluczowa przy projektowaniu konstrukcji, takich jak dachy trójkątne, gdzie obliczenia dotyczące pola są niezbędne do określenia obciążenia i stabilności. W przyszłości, z rosnącą popularnością technologii BIM (Building Information Modeling), dokładne obliczenia pól trójkątów będą jeszcze bardziej istotne, ponieważ pozwolą na integrację danych w czasie rzeczywistym, co z kolei ułatwi procesy projektowe i wykonawcze.

