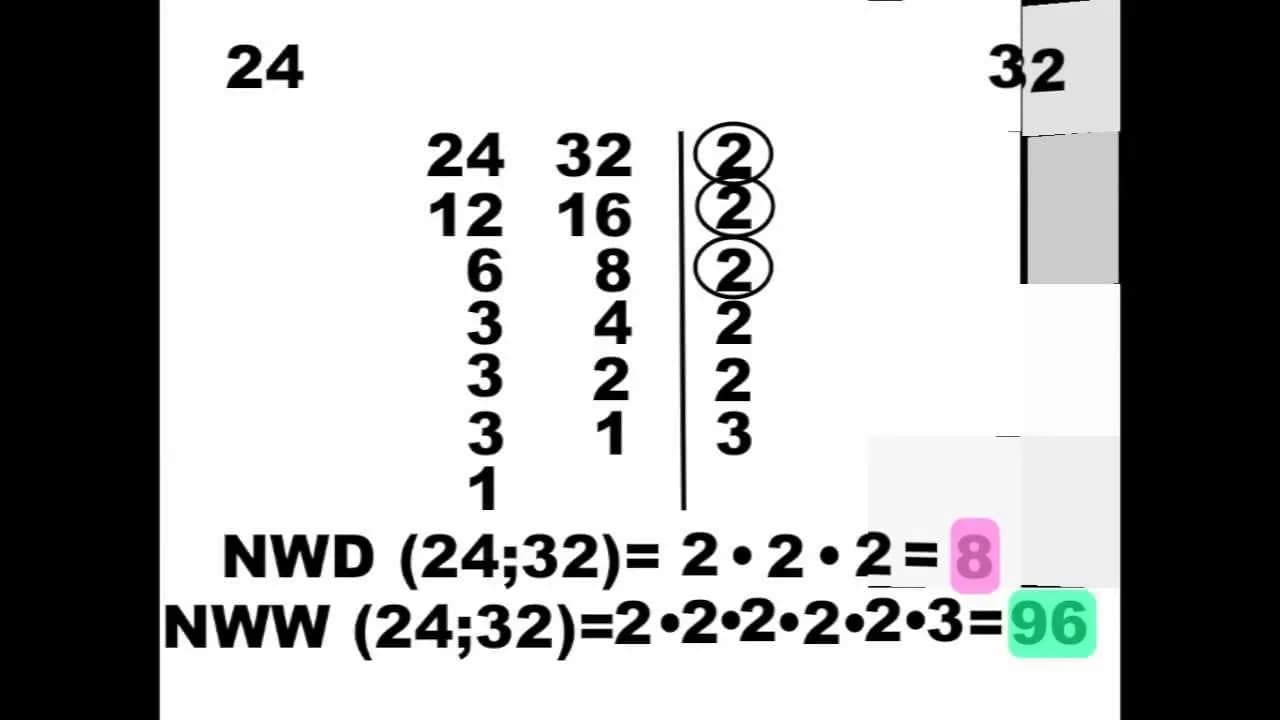
Najmniejsza wspólna wielokrotność (NWW) to fundamentalny koncept w matematyce, który odgrywa kluczową rolę w wielu dziedzinach, takich jak arytmetyka i algebra. NWW definiuje się jako najmniejsza liczba różna od zera, która jest wielokrotnością dwóch lub więcej liczb. Na przykład, dla liczb 4 i 6, NWW wynosi 12, ponieważ 12 jest najmniejszą liczbą, która jest wielokrotnością zarówno 4, jak i 6. Zrozumienie NWW jest nie tylko istotne w kontekście akademickim, ale także w codziennym życiu, gdzie może pomóc w rozwiązywaniu różnych problemów.
W artykule przyjrzymy się, jak obliczyć NWW, jakie metody można zastosować oraz jakie są praktyczne zastosowania tego pojęcia w matematyce i życiu codziennym. Poznanie NWW ułatwia zrozumienie bardziej złożonych zagadnień matematycznych i pozwala na efektywne rozwiązywanie problemów. Kluczowe informacje:- NWW to najmniejsza liczba, która jest wielokrotnością dwóch lub więcej liczb.
- Obliczanie NWW można przeprowadzić różnymi metodami, w tym przez rozkład na czynniki pierwsze.
- NWW jest istotne w matematyce, ponieważ pomaga w rozwiązywaniu równań i problemów arytmetycznych.
- Przykłady zastosowania NWW obejmują sytuacje w życiu codziennym, takie jak synchronizacja cykli czy planowanie wydarzeń.
Definicja najmniejszej wspólnej wielokrotności i jej znaczenie
Najmniejsza wspólna wielokrotność (NWW) to kluczowy termin w matematyce, który odnosi się do najmniejszej liczby różnej od zera, która jest wielokrotnością dwóch lub więcej liczb. Dla przykładu, dla liczb 4 i 6, NWW wynosi 12, ponieważ 12 jest najmniejszą liczbą, która jest wielokrotnością zarówno 4, jak i 6. Ta definicja jest fundamentalna w arytmetyce i algebra, ponieważ NWW jest często używane w problemach związanych z ułamkami oraz równaniami.
Zrozumienie NWW jest istotne nie tylko w teorii, ale również w praktyce. Pomaga w uproszczeniu obliczeń, co jest szczególnie ważne w zadaniach wymagających dodawania lub odejmowania ułamków. Dzięki NWW można znaleźć wspólny mianownik, co ułatwia dalsze operacje matematyczne.Co to jest NWW i jak jest definiowane w matematyce?
NWW, czyli najmniejsza wspólna wielokrotność, jest definiowana jako najmniejsza liczba, która jest wielokrotnością wszystkich podanych liczb. W matematyce, NWW można obliczyć na różne sposoby, jednak jego podstawowa definicja pozostaje niezmienna. Warto zauważyć, że NWW zawsze będzie liczbą całkowitą dodatnią, a dla każdej pary liczb całkowitych, NWW istnieje.
Właściwości NWW obejmują m.in. to, że jest zawsze większe lub równe największej z liczb, dla których jest obliczane. Ponadto, NWW dwóch liczb a i b można obliczyć za pomocą wzoru: NWW(a, b) = (a * b) / NWD(a, b), gdzie NWD to największy wspólny dzielnik. Ta relacja pokazuje, jak NWW jest powiązane z innymi kluczowymi pojęciami w matematyce.
Dlaczego znajomość NWW jest ważna w matematyce?
Zrozumienie najmniejszej wspólnej wielokrotności (NWW) jest kluczowe w matematyce, ponieważ ma szerokie zastosowanie w różnych kontekstach. NWW pozwala na łatwe rozwiązywanie problemów związanych z ułamkami, szczególnie w przypadku dodawania i odejmowania. Dzięki NWW możemy znaleźć wspólny mianownik dla różnych ułamków, co znacznie ułatwia dalsze obliczenia.
Ważność NWW nie ogranicza się tylko do teorii. W praktyce, znajomość NWW jest niezbędna w rozwiązywaniu równań oraz w analizie problemów matematycznych, gdzie trzeba znaleźć wspólne wielokrotności. W wielu zadaniach matematycznych, NWW staje się narzędziem, które umożliwia efektywne podejście do złożonych problemów.
Jak obliczyć najmniejszą wspólną wielokrotność krok po kroku
Aby obliczyć NWW, istnieje kilka metod, które można zastosować. Każda z nich ma swoje zalety i jest użyteczna w różnych sytuacjach. W tej sekcji omówimy kroki, które należy podjąć, aby skutecznie obliczyć NWW dla dwóch lub więcej liczb. Metody te obejmują m.in. rozkład na czynniki pierwsze oraz zastosowanie wzorów matematycznych.
- Rozkład na czynniki pierwsze - identyfikacja wszystkich czynników liczby i ich potęg.
- Użycie wzoru NWW(a, b) = (a * b) / NWD(a, b), gdzie NWD to największy wspólny dzielnik.
- Metoda tabeli, gdzie wypisujemy wielokrotności i szukamy najmniejszej wspólnej.
Metoda rozkładu na czynniki pierwsze do obliczania NWW
Metoda rozkładu na czynniki pierwsze to jedna z najskuteczniejszych technik obliczania najmniejszej wspólnej wielokrotności (NWW). Polega ona na rozłożeniu każdej z liczb na jej czynniki pierwsze, a następnie na wykorzystaniu tych czynników do znalezienia NWW. W tej metodzie, każdy czynnik jest brany pod uwagę z najwyższą potęgą, która występuje w rozkładzie wszystkich liczb.
Na przykład, aby obliczyć NWW dla liczb 12 i 18, najpierw rozkładamy je na czynniki pierwsze: 12 = 2² * 3¹, a 18 = 2¹ * 3². Następnie bierzemy każdy czynnik z najwyższą potęgą: 2² i 3². Mnożąc je razem, otrzymujemy NWW = 2² * 3² = 36. Ta metoda jest szczególnie przydatna, gdy mamy do czynienia z większymi liczbami lub z wieloma liczbami jednocześnie.
| Liczba | Rozkład na czynniki pierwsze | NWW |
| 12 | 2² * 3¹ | 36 |
| 18 | 2¹ * 3² | |
| 20 | 2² * 5¹ | 60 |
| 15 | 3¹ * 5¹ | |
| 30 | 2¹ * 3¹ * 5¹ |
Obliczanie NWW dla dwóch liczb - przykład praktyczny
Aby obliczyć NWW dla dwóch liczb, zastosujemy wcześniej omówioną metodę rozkładu na czynniki pierwsze. Weźmy na przykład liczby 8 i 12. Rozkładamy je na czynniki pierwsze: 8 = 2³, a 12 = 2² * 3¹. Następnie bierzemy każdy czynnik z najwyższą potęgą: 2³ oraz 3¹. Mnożąc te czynniki razem, uzyskujemy NWW = 2³ * 3¹ = 24.
Warto zauważyć, że ta metoda jest przejrzysta i łatwa do zastosowania. Dzięki niej możemy szybko obliczyć NWW dla dowolnych dwóch liczb, co jest niezwykle przydatne w wielu zadaniach matematycznych. W przypadku większej liczby liczb, proces pozostaje taki sam: rozkładamy każdą liczbę na czynniki pierwsze i wybieramy najwyższe potęgi dla każdego czynnika.
Czytaj więcej: Jak pomóc dziecku, które nie chce chodzić do szkoły? 5 porad
Przykłady zastosowania NWW w matematyce i codziennym życiu

Zastosowanie najmniejszej wspólnej wielokrotności (NWW) w matematyce jest niezwykle szerokie i obejmuje różnorodne konteksty, zarówno te teoretyczne, jak i praktyczne. NWW jest używane w zadaniach związanych z ułamkami, gdzie konieczne jest znalezienie wspólnego mianownika. Dzięki temu, dodawanie czy odejmowanie ułamków staje się znacznie prostsze i bardziej zrozumiałe. W codziennym życiu NWW również odgrywa ważną rolę, na przykład w planowaniu harmonogramów czy przydzielaniu zasobów.
W matematyce, NWW jest kluczowe w rozwiązywaniu problemów, które wymagają synchronizacji różnych cykli lub okresów. Przykładem może być sytuacja, w której dwie osoby mają różne harmonogramy i chcą ustalić, kiedy będą miały wspólny czas na spotkanie. W takich przypadkach, obliczenie NWW cykli pozwala na znalezienie optymalnego momentu na spotkanie.
Zastosowanie NWW w rozwiązywaniu problemów matematycznych
W matematyce, NWW można wykorzystać do rozwiązywania różnorodnych problemów, które wymagają zrozumienia relacji między liczbami. Przykładowo, w zadaniach dotyczących ułamków, NWW pozwala na znalezienie wspólnego mianownika, co jest niezbędne do wykonania operacji arytmetycznych. Dzięki temu, uczniowie mogą łatwiej zrozumieć, jak dodawać lub odejmować ułamki o różnych mianownikach.
- Przykład 1: Obliczenie NWW dla liczb 8 i 12, aby dodać ułamki 1/8 i 1/12.
- Przykład 2: Ustalenie wspólnego cyklu dwóch maszyn, które pracują co 4 i 6 dni, aby zaplanować konserwację.
- Przykład 3: Rozwiązywanie problemów dotyczących harmonogramów, gdzie różne zadania powtarzają się co 3, 5 i 7 dni.
| Problem | Opis |
| Dodawanie ułamków | Użycie NWW do znalezienia wspólnego mianownika dla 1/4 i 1/6. |
| Planowanie spotkań | Obliczenie NWW dla cykli 5 dni i 7 dni, aby ustalić datę spotkania. |
| Synchronizacja zadań | Ustalenie NWW dla zadań powtarzających się co 2, 3 i 4 dni. |
NWW w kontekście życia codziennego - przykłady praktyczne
Najmniejsza wspólna wielokrotność (NWW) ma wiele zastosowań w codziennym życiu, które pomagają w organizacji i planowaniu. Przykłady te pokazują, jak matematyka wpływa na nasze decyzje i działania. Na przykład, w przypadku dwóch osób, które chcą zorganizować spotkanie, a jedna z nich ma wolne dni co 5 dni, a druga co 7 dni, NWW pozwoli im określić, kiedy obie będą miały wolny czas. W tym przypadku NWW wynosi 35, co oznacza, że spotkanie może odbyć się co 35 dni.
Kolejnym praktycznym zastosowaniem NWW jest planowanie wydarzeń, takich jak zajęcia sportowe czy zajęcia w szkole, które odbywają się w różnych cyklach. Na przykład, jeśli jedna klasa ma zajęcia co 3 dni, a inna co 4 dni, NWW pomoże ustalić, kiedy obie klasy będą miały wspólne zajęcia. W tym przypadku NWW wynosi 12, co oznacza, że obie klasy spotkają się co 12 dni.
- Przykład 1: Synchronizacja harmonogramów dwóch osób pracujących na zmianę co 6 i 8 dni.
- Przykład 2: Ustalanie daty konserwacji sprzętu, który wymaga przeglądu co 15 i 20 dni.
- Przykład 3: Planowanie spotkań dla grupy, gdzie członkowie mają różne dni dostępności, np. co 2, 3 i 5 dni.
Wykorzystanie NWW w programowaniu i analizie danych
W kontekście nowoczesnych technologii, najmniejsza wspólna wielokrotność (NWW) ma zastosowanie nie tylko w matematyce, ale także w programowaniu i analizie danych. Programiści często muszą synchronizować różne procesy lub zadania, które mogą występować w różnych cyklach. W takich sytuacjach, obliczanie NWW pozwala na efektywne zarządzanie czasem oraz zasobami, co jest kluczowe w tworzeniu wydajnych algorytmów. Na przykład, w aplikacjach mobilnych, które wymagają synchronizacji danych z serwerem, NWW może być użyte do określenia, jak często aplikacja powinna pobierać aktualizacje, aby uniknąć konfliktów.Dodatkowo, w analizie danych, NWW może być wykorzystane do przetwarzania informacji z różnych źródeł, które operują na różnych interwałach czasowych. Zrozumienie, jak te interwały się pokrywają, pozwala na lepsze modelowanie danych oraz przewidywanie trendów. Na przykład, w analizie sprzedaży, gdzie dane są zbierane co tydzień i co miesiąc, NWW pomoże w ustaleniu, kiedy najlepiej analizować dane, aby uzyskać pełniejszy obraz sytuacji rynkowej.