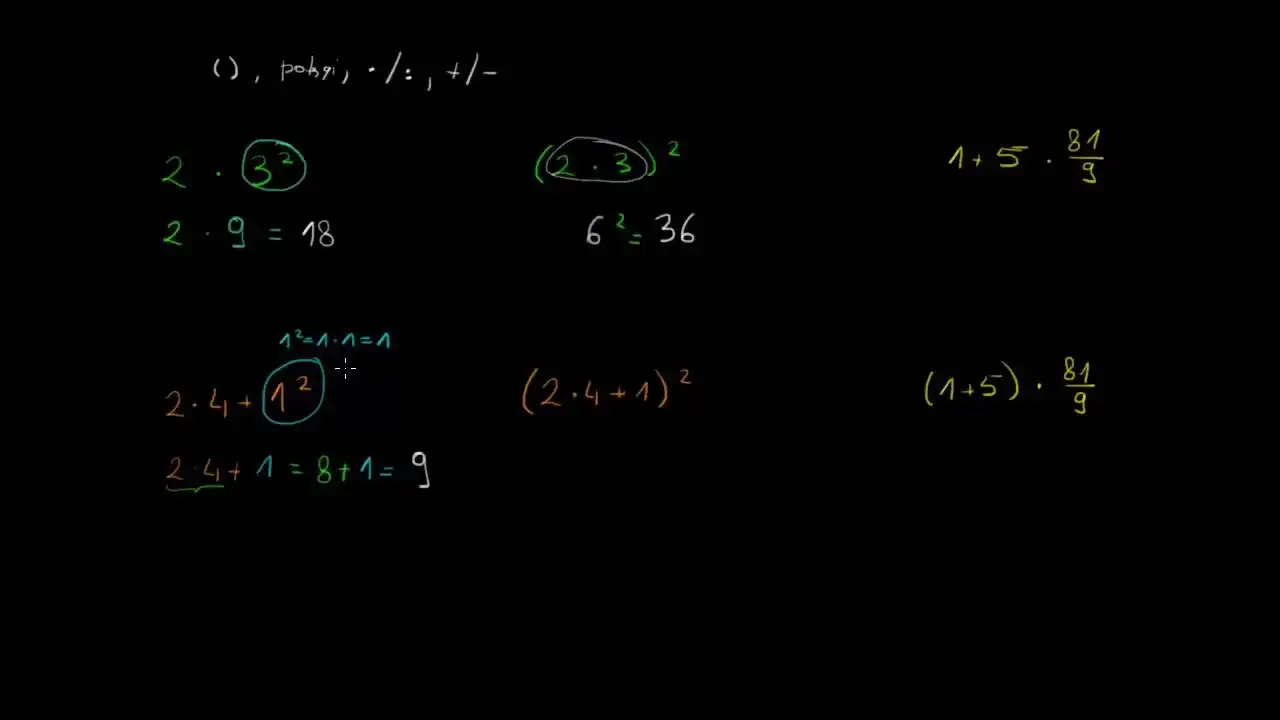Nawias kwadratowy w matematyce odgrywa kluczową rolę w organizowaniu i grupowaniu wyrażeń. Używamy go, aby określić, które działania należy wykonać w pierwszej kolejności, co jest niezwykle ważne dla uzyskania poprawnych wyników. W sytuacjach, gdy mamy do czynienia z wieloma nawiasami, nawiasy kwadratowe często pełnią funkcję nawiasów zewnętrznych, podczas gdy nawiasy okrągłe są używane wewnątrz. Dzięki temu możemy lepiej odwzorować hierarchię działań matematycznych.
W tym artykule przyjrzymy się bliżej funkcji nawiasów kwadratowych, ich znaczeniu w matematyce oraz porównamy je z innymi typami nawiasów. Zrozumienie, jak i kiedy stosować nawiasy, pomoże w uniknięciu błędów podczas rozwiązywania złożonych wyrażeń matematycznych.
Kluczowe informacje:- Nawiasy kwadratowe grupują wyrażenia, co pomaga w ustaleniu kolejności działań.
- Są często używane jako nawiasy zewnętrzne, gdy wewnątrz znajdują się nawiasy okrągłe.
- Ich właściwe zastosowanie jest kluczowe dla uzyskania poprawnych wyników w matematyce.
- Porównanie nawiasów kwadratowych, okrągłych i klamrowych ujawnia ich różne funkcje i zastosowania.
- Wizualne przedstawienia nawiasów mogą ułatwić zrozumienie ich działania w złożonych wyrażeniach.
Nawiasy kwadratowe w matematyce: ich rola i znaczenie
Nawiasy kwadratowe są niezwykle ważnym elementem w matematyce, ponieważ służą do grupowania wyrażeń oraz określenia kolejności wykonywania działań. Użycie nawiasów kwadratowych pomaga w organizacji złożonych obliczeń, co jest kluczowe dla uzyskania poprawnych wyników. Dzięki nim możemy jasno wskazać, które działania powinny być wykonane najpierw, co jest niezbędne w matematyce.
W przypadku skomplikowanych wyrażeń matematycznych, nawiasy kwadratowe często pełnią funkcję nawiasów zewnętrznych, podczas gdy inne typy nawiasów, takie jak nawiasy okrągłe, są używane wewnątrz. Taki układ pozwala na lepsze odwzorowanie hierarchii działań. Przykładowo, w wyrażeniu matematycznym 2 * [3 + (4 - 1)], nawiasy kwadratowe wskazują, że najpierw należy obliczyć wyrażenie w nawiasie okrągłym, a następnie dodać wynik do liczby 3.
Jak nawiasy kwadratowe grupują wyrażenia matematyczne
Nawiasy kwadratowe grupują wyrażenia matematyczne, co pozwala na klarowne przedstawienie obliczeń. Umożliwiają one zorganizowanie działań w taki sposób, aby uniknąć nieporozumień i błędów w obliczeniach. Na przykład, w wyrażeniu 5 * [2 + 3], nawias kwadratowy wskazuje, że najpierw należy dodać 2 i 3, a dopiero potem pomnożyć wynik przez 5.
- Użycie nawiasów kwadratowych poprawia przejrzystość złożonych wyrażeń matematycznych.
- Grupowanie działań w nawiasach kwadratowych pomaga w unikaniu błędów obliczeniowych.
- Nawiasy kwadratowe są kluczowe w kontekście hierarchii działań matematycznych.
Dlaczego nawiasy kwadratowe są kluczowe w kolejności działań
Nawiasy kwadratowe odgrywają istotną rolę w kolejności działań matematycznych. Umożliwiają one zrozumienie, które operacje należy wykonać w pierwszej kolejności, co jest kluczowe dla uzyskania poprawnych wyników. W matematyce, stosowanie nawiasów kwadratowych pozwala na jasne wskazanie, że działania wewnątrz nawiasów powinny być zrealizowane przed innymi operacjami, co zapobiega pomyłkom.
Na przykład, w wyrażeniu 3 + [2 * (4 - 1)], nawiasy kwadratowe wskazują, że najpierw musimy obliczyć wyrażenie w nawiasie okrągłym, a następnie wynik pomnożyć przez 2 przed dodaniem 3. Bez użycia nawiasów kwadratowych, moglibyśmy zinterpretować to wyrażenie błędnie. Dlatego nawiasy kwadratowe są kluczowe dla poprawnego zrozumienia i wykonywania działań matematycznych.
Porównanie nawiasów kwadratowych z innymi typami nawiasów
W matematyce istnieje wiele typów nawiasów, w tym nawiasy kwadratowe, okrągłe i klamrowe, które mają różne zastosowania. Nawiasy kwadratowe są używane głównie do grupowania wyrażeń i wskazywania kolejności działań, podczas gdy nawiasy okrągłe często służą do wskazywania argumentów funkcji lub operacji. Nawiasy klamrowe są z kolei używane w kontekście zbiorów lub do grupowania elementów w bardziej złożonych strukturach matematycznych.
Ważne jest, aby zrozumieć różnice między tymi typami nawiasów, ponieważ ich niewłaściwe użycie może prowadzić do błędów w obliczeniach. Nawiasy kwadratowe, okrągłe i klamrowe mają swoje unikalne funkcje, które są kluczowe dla poprawności matematycznych wyrażeń.
Różnice między nawiasami kwadratowymi a okrągłymi
Nawiasy kwadratowe i okrągłe pełnią różne funkcje w matematyce, co jest istotne dla dokładności obliczeń. Nawiasy kwadratowe są głównie używane do grupowania wyrażeń oraz wskazywania kolejności działań, podczas gdy nawiasy okrągłe najczęściej służą do definiowania argumentów funkcji lub do grupowania operacji wewnątrz innych nawiasów. Na przykład w wyrażeniu 5 * [2 + (3 - 1)], nawiasy okrągłe wskazują, że najpierw należy obliczyć 3 - 1, a następnie dodać wynik do 2, a całość pomnożyć przez 5.
Warto również zauważyć, że nawiasy kwadratowe mogą być używane jako nawiasy zewnętrzne, gdy wewnątrz znajdują się nawiasy okrągłe. Dzięki temu można lepiej zorganizować złożone wyrażenia matematyczne. W przeciwieństwie do tego, nawiasy okrągłe nie mają takiej samej funkcji w hierarchii działań, co sprawia, że ich zastosowanie jest bardziej ograniczone w kontekście grupowania wyrażeń.
Kiedy i jak stosować nawiasy klamrowe w matematyce
Nawiasy klamrowe, oznaczane jako { }, są używane w matematyce do definiowania zbiorów oraz do grupowania elementów w bardziej złożonych strukturach. Stosowanie nawiasów klamrowych jest szczególnie istotne w kontekście teorii zbiorów, gdzie pozwalają one na wyraźne określenie, które elementy należą do danego zbioru. Na przykład, zapis {1, 2, 3} oznacza zbiór zawierający liczby 1, 2 i 3.W praktyce, nawiasy klamrowe mogą być również używane w programowaniu i w różnych dziedzinach matematyki, takich jak algebra, gdzie grupują wyrażenia lub definiują zbiory. Ważne jest, aby pamiętać, że nawiasy klamrowe nie są stosowane w ten sam sposób co nawiasy kwadratowe czy okrągłe, dlatego ich zastosowanie powinno być dobrze zrozumiane, aby uniknąć błędów w obliczeniach.
Czytaj więcej: Najlepsze zajęcia dydaktyczne w żłobku: 15 skutecznych pomysłów na rozwój
Hierarchia działań matematycznych: znaczenie nawiasów
W matematyce istnieje określona hierarchia działań, która określa kolejność, w jakiej należy wykonywać różne operacje, aby uzyskać poprawny wynik. Nawiasy, w tym nawiasy kwadratowe, odgrywają kluczową rolę w tej hierarchii, ponieważ pozwalają na grupowanie działań i wskazywanie, które operacje powinny być wykonane najpierw. Dzięki nim można zorganizować złożone wyrażenia matematyczne w sposób, który zapobiega błędom i nieporozumieniom. Właściwe zrozumienie hierarchii działań jest niezbędne do skutecznego rozwiązywania problemów matematycznych.
Nawiasy kwadratowe są używane jako elementy zewnętrzne, które mogą obejmować inne nawiasy, co pozwala na tworzenie bardziej złożonych struktur matematycznych. W ten sposób, nawiasy kwadratowe nie tylko pomagają w grupowaniu działań, ale także w ustalaniu, które z nich mają pierwszeństwo. W kontekście hierarchii działań, nawiasy kwadratowe są traktowane równorzędnie z nawiasami okrągłymi, co podkreśla ich znaczenie w matematycznych obliczeniach.
Jak nawiasy kwadratowe wpływają na wynik końcowy
Użycie nawiasów kwadratowych ma bezpośredni wpływ na wynik końcowy działań matematycznych. Gdy nawiasy kwadratowe są stosowane w wyrażeniach, określają one, które operacje powinny być wykonane w pierwszej kolejności. Na przykład, w wyrażeniu 2 + [3 * (4 - 1)], nawiasy kwadratowe wskazują, że najpierw należy obliczyć 3 * (4 - 1), a dopiero potem dodać 2, co prowadzi do innego wyniku, niż gdyby operacje były wykonywane w innej kolejności.
Warto zauważyć, że zignorowanie nawiasów kwadratowych lub ich niewłaściwe użycie może prowadzić do błędów w obliczeniach. Dlatego zrozumienie, jak nawiasy kwadratowe wpływają na wynik końcowy, jest kluczowe dla każdego, kto zajmuje się matematyką. Nawiasy kwadratowe są nie tylko narzędziem do grupowania wyrażeń, ale także fundamentalnym elementem, który wpływa na poprawność wyników obliczeń.
Przykłady zastosowania nawiasów w złożonych wyrażeniach
Nawiasy kwadratowe są niezwykle przydatne w złożonych wyrażeniach matematycznych, gdzie ich odpowiednie zastosowanie może znacząco wpłynąć na wynik obliczeń. Na przykład, w wyrażeniu 2 * [3 + (4 - 1)], nawiasy kwadratowe wskazują, że najpierw należy obliczyć wartość w nawiasie okrągłym, a następnie dodać wynik do 3, a całość pomnożyć przez 2. Bez użycia nawiasów kwadratowych, moglibyśmy zinterpretować to wyrażenie błędnie.Inny przykład to wyrażenie [5 + (2 * 3)] - 4, w którym nawiasy kwadratowe wskazują, że najpierw wykonujemy mnożenie, a następnie dodawanie, a dopiero na końcu odejmowanie. Taka struktura pozwala na jasne i poprawne obliczenia. Poniżej przedstawiamy tabelę z różnymi wyrażeniami, które ilustrują rolę nawiasów kwadratowych w matematyce.
| Wyrażenie | Wynik |
|---|---|
| 2 * [3 + (4 - 1)] | 10 |
| [5 + (2 * 3)] - 4 | 10 |
| 3 * [2 + (8 / 4)] | 15 |
| [10 - (3 + 2)] * 2 | 10 |
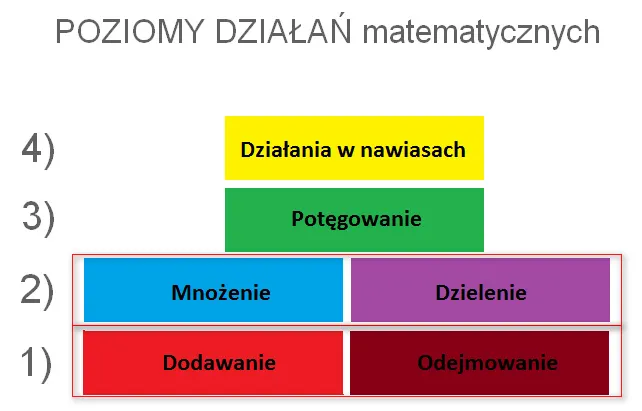
Wizualne przedstawienie użycia nawiasów kwadratowych
Wizualizacja to potężne narzędzie w matematyce, które pomaga w zrozumieniu złożonych pojęć, takich jak nawiasy kwadratowe. Dzięki diagramom i graficznym przedstawieniom, możemy lepiej zobaczyć, jak nawiasy wpływają na kolejność działań oraz na wyniki obliczeń. Wizualne przedstawienia umożliwiają szybkie zrozumienie, które operacje są grupowane i jakie mają pierwszeństwo w obliczeniach.
Diagramy ilustrujące działanie nawiasów w matematyce
Diagramy są doskonałym sposobem na ilustrowanie działania nawiasów kwadratowych w matematyce. Na przykład, diagramy mogą pokazywać, jak różne nawiasy wpływają na wynik końcowy wyrażenia. Przykładowo, w diagramie przedstawiającym wyrażenie 2 * [3 + (4 - 1)], można wizualnie zaznaczyć, które działania są wykonywane najpierw, co ułatwia zrozumienie hierarchii działań.
Praktyczne zastosowania nawiasów kwadratowych w programowaniu
Nawiasy kwadratowe nie tylko odgrywają kluczową rolę w matematyce, ale również mają istotne zastosowanie w programowaniu. W wielu językach programowania, takich jak Python czy JavaScript, nawiasy kwadratowe są używane do definiowania tablic i list, co pozwala na efektywne przechowywanie i manipulowanie danymi. Na przykład, w Pythonie, lista [1, 2, 3] jest zbiorem wartości, które można łatwo przeszukiwać, modyfikować i analizować, co czyni nawiasy kwadratowe niezwykle przydatnymi w codziennej pracy programisty.
Warto również zauważyć, że w kontekście programowania funkcyjnego, nawiasy kwadratowe mogą być używane do definiowania funkcji wyższego rzędu, co pozwala na bardziej złożone operacje na danych. Zrozumienie, jak korzystać z nawiasów kwadratowych w programowaniu, otwiera drzwi do bardziej zaawansowanych technik i umożliwia tworzenie bardziej złożonych algorytmów, co może znacznie zwiększyć efektywność kodu i jego czytelność.