Silnia to fundamentalna operacja w matematyce, która polega na mnożeniu wszystkich kolejnych liczb całkowitych od 1 do określonej liczby całkowitej n. Symbol silni to "!". Na przykład, silnia z 5, zapisywana jako 5!, wynosi 120, ponieważ obliczamy ją jako 5 * 4 * 3 * 2 * 1. Zrozumienie silni jest nie tylko istotne dla uczniów, ale także stanowi fundament wielu bardziej zaawansowanych koncepcji matematycznych.
W artykule przyjrzymy się, jak obliczać silnię oraz jakie ma ona znaczenie w różnych dziedzinach matematyki, w tym w kombinatoryce i statystyce. Wiedza na temat silni jest niezbędna do rozwiązywania problemów związanych z permutacjami i kombinacjami, które są powszechnie stosowane w naukach ścisłych i informatyce.
Kluczowe informacje:- Silnia to iloczyn wszystkich liczb całkowitych od 1 do n, oznaczany symbolem "!".
- Obliczanie silni jest istotne w matematyce, szczególnie w kombinatoryce i statystyce.
- Silnia jest używana do rozwiązywania problemów związanych z permutacjami i kombinacjami.
- Zrozumienie silni pomaga uczniom w nauce bardziej zaawansowanych koncepcji matematycznych.
- Przykłady obliczeń silni dla małych i dużych liczb ilustrują jej praktyczne zastosowanie.
Definicja silni w matematyce i jej znaczenie dla uczniów
Silnia to matematyczna operacja, która polega na pomnożeniu wszystkich kolejnych liczb całkowitych od 1 do danej liczby całkowitej n. Symbol silni to "!". Na przykład, silnia z 5, zapisywana jako 5!, wynosi 120, co można obliczyć jako 5 * 4 * 3 * 2 * 1. Ta operacja jest niezwykle istotna w matematyce, ponieważ stanowi podstawę wielu bardziej skomplikowanych koncepcji.
Wiedza na temat silni jest kluczowa dla uczniów, ponieważ pomaga w zrozumieniu bardziej zaawansowanych tematów, takich jak kombinacje i permutacje. Dzięki silni uczniowie mogą lepiej zrozumieć, jak liczby są ze sobą powiązane oraz jak można je wykorzystać w praktycznych problemach matematycznych. Zrozumienie tej koncepcji otwiera drzwi do wielu dziedzin naukowych, w tym statystyki i teorii prawdopodobieństwa.
Co to jest silnia i jak ją zrozumieć w prosty sposób
Silnia, oznaczana symbolem "!", jest operacją, która oblicza iloczyn wszystkich liczb całkowitych od 1 do n. Na przykład, silnia z 3, czyli 3!, to 3 * 2 * 1, co daje 6. Warto zauważyć, że silnia z 0, zapisywana jako 0!, wynosi 1, co jest definicją umowną w matematyce. Ta operacja jest stosunkowo prosta do zrozumienia, a jej notacja jest powszechnie używana w różnych dziedzinach matematyki.
Dlaczego silnia jest kluczowa w matematyce i naukach ścisłych
Silnia odgrywa fundamentalną rolę w matematyce oraz naukach ścisłych, ponieważ jest niezbędna do zrozumienia wielu koncepcji związanych z kombinacjami i permutacjami. Umożliwia ona obliczanie liczby sposobów, w jakie można zorganizować lub wybrać elementy z danej grupy, co jest kluczowe w statystyce, teorii prawdopodobieństwa i informatyce. Dzięki silni uczniowie mogą lepiej zrozumieć, jak liczby są ze sobą powiązane oraz jak można je wykorzystać w praktycznych problemach matematycznych. Zrozumienie tej koncepcji otwiera drzwi do bardziej zaawansowanych tematów, takich jak analiza danych czy algorytmy. W związku z tym, nauka o silni jest istotnym krokiem w edukacji matematycznej, który wspiera rozwój umiejętności analitycznych uczniów.
Jak obliczyć silnię krok po kroku dla różnych liczb
Obliczanie silni może wydawać się skomplikowane, ale istnieją proste metody, które można zastosować do różnych liczb całkowitych. Silnię można obliczyć na dwa główne sposoby: poprzez metodę iteracyjną oraz metodę rekurencyjną. Metoda iteracyjna polega na wykorzystaniu pętli do mnożenia kolejnych liczb całkowitych, podczas gdy metoda rekurencyjna wykorzystuje funkcje wywołujące same siebie, aby obliczyć wartość silni. Obie metody prowadzą do tego samego wyniku, ale różnią się podejściem i zastosowaniem w programowaniu.Warto również znać podstawowe wartości silni dla najczęściej używanych liczb. Poniżej znajduje się lista silni dla liczb od 0 do 10:
- 0! = 1
- 1! = 1
- 2! = 2
- 3! = 6
- 4! = 24
- 5! = 120
- 6! = 720
- 7! = 5040
- 8! = 40320
- 9! = 362880
- 10! = 3628800
Metoda obliczania silni dla liczb całkowitych od 1 do n
Obliczanie silni można przeprowadzić na dwa główne sposoby: metodą iteracyjną oraz metodą rekurencyjną. Metoda iteracyjna polega na użyciu pętli, która mnoży kolejne liczby całkowite, zaczynając od 1 aż do n. Na przykład, aby obliczyć 5!, program mógłby wyglądać tak: zaczynamy od zmiennej wynikowej równej 1, a następnie w pętli mnożymy ją przez każdą liczbę od 1 do 5. W ten sposób uzyskujemy wynik 120.
Metoda rekurencyjna polega na tym, że funkcja wywołuje samą siebie, aż osiągnie wartość bazową. Dla silni, wartością bazową jest 0! = 1 oraz 1! = 1. Funkcja może wyglądać następująco: silnia(n) = n * silnia(n-1). Dzięki tej metodzie, obliczając 5!, funkcja najpierw wywoła się dla 4, potem dla 3, i tak dalej, aż dotrze do 1, a następnie zacznie zwracać wyniki, mnożąc je ze sobą.
Przykłady obliczeń silni dla małych i dużych liczb
Obliczanie silni dla małych liczb jest dość proste i można to zrobić ręcznie. Na przykład, 4! obliczamy jako 4 * 3 * 2 * 1, co daje 24. Z kolei dla liczby 6, mamy 6! = 6 * 5 * 4 * 3 * 2 * 1, co daje nam 720. Te proste obliczenia pomagają zrozumieć, jak działa silnia i jak można ją wykorzystać w różnych kontekstach matematycznych.
| Liczba | Silnia |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
Czytaj więcej: Kursy języka hiszpańskiego w Chile: najskuteczniejsze metody nauki
Zastosowanie silni w matematyce: od kombinacji do permutacji
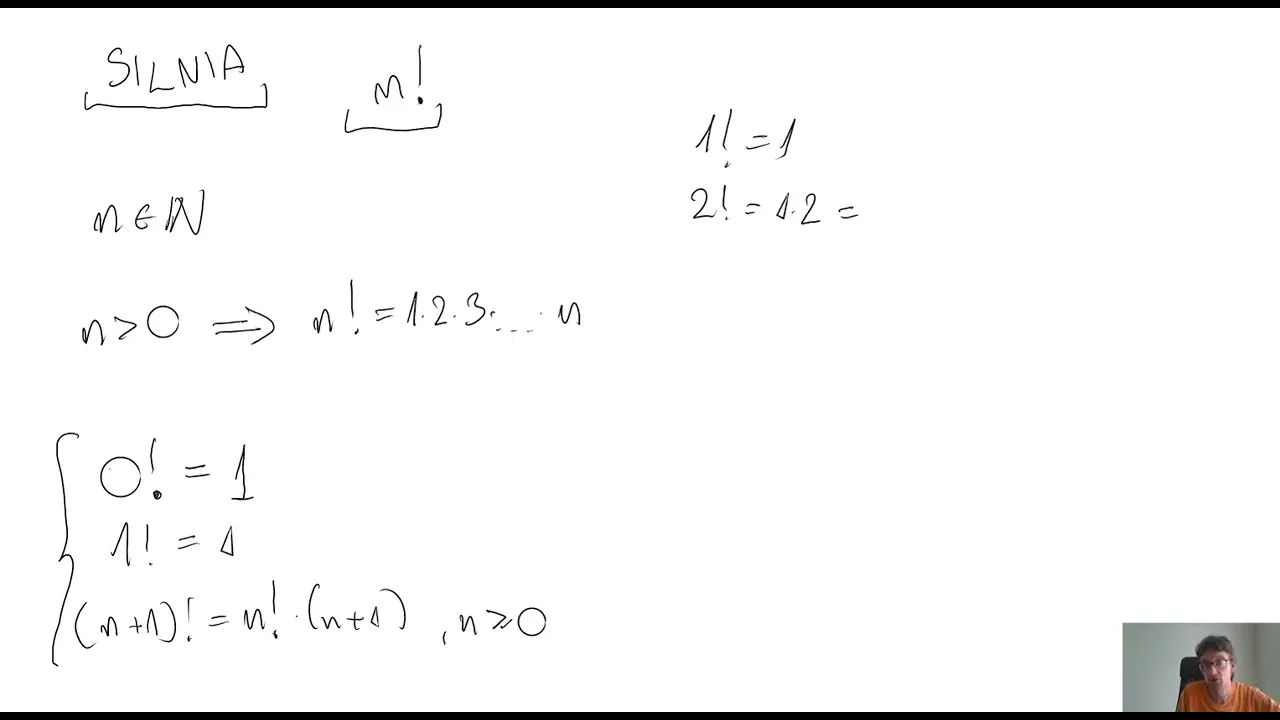
Silnia ma kluczowe znaczenie w różnych dziedzinach matematyki, szczególnie w kombinatoryce i permutacjach. Umożliwia obliczanie liczby sposobów, w jakie można zorganizować lub wybrać elementy z danej grupy. Na przykład, w problemach dotyczących układania przedmiotów w określonej kolejności, silnia pozwala na określenie, ile różnych kombinacji można stworzyć. W praktyce, silnia jest wykorzystywana w statystyce do obliczania prawdopodobieństw oraz w informatyce w algorytmach sortujących i wyszukujących.
W kontekście kombinacji, silnia jest używana do obliczania liczby sposobów wyboru k elementów z n elementów, co jest wyrażane wzorem: C(n, k) = n! / (k! * (n-k)!). W ten sposób, silnia nie tylko ułatwia zrozumienie struktury matematycznej, ale także pozwala na praktyczne zastosowanie w rozwiązywaniu problemów. Zrozumienie zastosowania silni w tych dziedzinach jest kluczowe dla uczniów, którzy pragną rozwijać swoje umiejętności analityczne i logiczne myślenie.
Jak silnia wspiera rozwiązywanie problemów kombinatorycznych
Silnia jest niezbędna w rozwiązywaniu problemów kombinatorycznych, ponieważ pozwala na dokładne obliczenie liczby możliwych układów elementów. Na przykład, jeśli mamy 5 różnych książek i chcemy wiedzieć, na ile sposobów możemy je ułożyć na półce, używamy silni: 5! = 120. To oznacza, że istnieje 120 różnych sposobów na ułożenie tych książek. Tego typu problemy są powszechne w matematyce i naukach komputerowych, gdzie analiza możliwości jest kluczowa.
Innym przykładem zastosowania silni w problemach kombinatorycznych jest obliczanie liczby sposobów, w jakie można wybrać grupę osób z większej liczby. Na przykład, jeśli mamy 10 osób i chcemy wybrać 3, to liczba możliwości wynosi C(10, 3) = 10! / (3! * 7!) = 120. Takie obliczenia są niezwykle przydatne w statystyce, badaniach społecznych i planowaniu wydarzeń, gdzie ważne jest zrozumienie różnych kombinacji.
Przykłady zastosowania silni w praktycznych zadaniach matematycznych
Silnia znajduje zastosowanie w wielu praktycznych zadaniach matematycznych, szczególnie w analizie danych i statystyce. Przykładem może być problem obliczania prawdopodobieństwa w grze karcianej. Jeśli mamy 52 karty w talii i chcemy obliczyć, na ile sposobów możemy wybrać 5 kart, używamy kombinacji, która wykorzystuje silnię: C(52, 5) = 52! / (5! * 47!). To obliczenie pozwala nam określić, ile różnych układów kart możemy otrzymać, co jest kluczowe w strategiach gier. Innym przykładem zastosowania silni jest analiza rozkładów statystycznych. Na przykład, w badaniach dotyczących rozkładu normalnego, silnia jest używana do obliczania wartości funkcji gęstości prawdopodobieństwa. Używając silni, możemy obliczyć liczbę sposobów, w jakie dane mogą być zorganizowane, co jest istotne w analizie danych i podejmowaniu decyzji opartych na statystyce. Takie zastosowania silni pokazują, jak istotna jest ta operacja w praktycznych problemach matematycznych i naukowych.Nowe zastosowania silni w analizie danych i uczeniu maszynowym
W miarę jak świat staje się coraz bardziej złożony, silnia zyskuje nowe zastosowania w analizie danych i uczeniu maszynowym. W kontekście algorytmów klasyfikacji i regresji, silnia jest wykorzystywana do obliczania prawdopodobieństw w modelach statystycznych, takich jak regresja logistyczna. W takich przypadkach, silnia pomaga w określeniu liczby możliwych wyników, co jest kluczowe dla przewidywania wyników na podstawie danych wejściowych. Warto zauważyć, że w miarę wzrostu złożoności modeli, umiejętność efektywnego obliczania silni staje się niezbędna dla analityków danych.
Dodatkowo, w kontekście big data, silnia może być używana do optymalizacji algorytmów przetwarzających ogromne zbiory danych. Na przykład, w algorytmach wyszukiwania i sortowania, silnia może pomóc w określeniu liczby możliwych kombinacji do przetworzenia, co z kolei wpływa na wydajność obliczeń. W przyszłości, z rozwojem technologii obliczeniowych, możemy spodziewać się jeszcze bardziej zaawansowanych zastosowań silni, które będą wspierać innowacyjne podejścia w analizie danych i rozwoju sztucznej inteligencji.





