Granica funkcji i ciągu: Jak obliczyć? Wyjaśnienie i przykłady

Granica to jedno z fundamentalnych pojęć w matematyce, stanowiące kamień węgielny analizy matematycznej. Jej zrozumienie jest kluczowe dla każdego ucznia i studenta, który chce nie tylko poprawnie rozwiązywać zadania, ale przede wszystkim głęboko pojąć, jak zachowują się funkcje i ciągi, zwłaszcza w kontekście ich dążenia do określonych wartości lub nieskończoności. Bez solidnych podstaw w zakresie granic, dalsza nauka rachunku różniczkowego i całkowego staje się znacznie trudniejsza.

Granica: Co to jest i dlaczego jest tak ważna w matematyce?

Pojęcie granicy jest jednym z najbardziej fundamentalnych i zarazem abstrakcyjnych w całej matematyce. W najprostszym ujęciu opisuje ono zachowanie pewnej wielkości, gdy inna wielkość zbliża się do pewnej wartości. To właśnie dzięki granicom możemy analizować nieskończenie małe zmiany, badać zachowanie funkcji w punktach, gdzie są one niezdefiniowane, czy opisywać procesy, które nigdy się nie kończą. Bez tego narzędzia analiza matematyczna, a co za tym idzie, wiele dziedzin nauki i techniki, wyglądałaby zupełnie inaczej.

Wyobraźmy sobie samochód przyspieszający do maksymalnej prędkości. W każdym momencie jego prędkość jest inna, ale dąży do pewnej wartości granicznej. Albo gdy zbliżamy się do celu podróży pokonujemy kolejne metry, ale jesteśmy coraz bliżej, choć sam moment dotarcia jest pewnym "punktem granicznym". Granica matematyczna formalizuje tę ideę "zbliżania się" lub "dążenia" do czegoś, co może, ale nie musi, zostać ostatecznie osiągnięte.

Współczesna nauka i technika opierają się w ogromnej mierze na analizie matematycznej, a jej sercem jest właśnie pojęcie granicy. To dzięki niej możemy precyzyjnie opisać i obliczyć prędkość chwilową obiektu (pochodna), wyznaczyć pole pod krzywą (całka), analizować stabilność systemów, optymalizować procesy produkcyjne czy modelować zjawiska fizyczne, od ruchu planet po zachowanie cząstek elementarnych. Bez granic nie byłoby zaawansowanego rachunku różniczkowego i całkowego, które są narzędziami niezbędnymi w inżynierii, fizyce, ekonomii, informatyce i wielu innych dziedzinach.

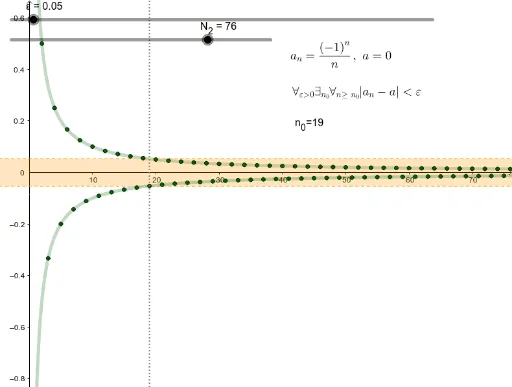
Granica ciągu: Podróż w nieskończoność

Ciąg liczbowy to po prostu uporządkowany zbiór liczb, często zapisywany jako $a_1, a_2, a_3, \dots, a_n, \dots$. Myśląc o granicy ciągu, zastanawiamy się, co dzieje się z jego wyrazami, gdy numer wyrazu $n$ staje się coraz większy, czyli gdy "idziemy w nieskończoność". Czy wyrazy ciągu zaczynają się zachowywać w przewidywalny sposób, zbliżając się do pewnej konkretnej liczby?

Kiedy mówimy, że ciąg $(a_n)$ ma granicę $g$, tak naprawdę chcemy powiedzieć, że od pewnego momentu wszystkie kolejne wyrazy ciągu są już bardzo blisko liczby $g$. Nie muszą być one równe $g$, ale znajdują się w dowolnie małym "przedziale" wokół $g$. Wyobraź sobie, że masz cel, a każdy kolejny krok przybliża Cię do niego coraz bardziej, choć nigdy go nie osiągasz. W matematyce mówimy, że "prawie wszystkie" wyrazy ciągu znajdują się w dowolnie wybranym, małym otoczeniu liczby $g$. To właśnie ta idea "bliskości" jest kluczowa dla zrozumienia granicy ciągu.

Przyjrzyjmy się kilku przykładom, aby lepiej zrozumieć, czym jest zbieżność i rozbieżność ciągu:

• Ciąg zbieżny: $a_n = \frac{1}{n}$. Wyrazy tego ciągu to: $1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \dots$. Jak widać, gdy $n$ rośnie, $\frac{1}{n}$ staje się coraz mniejsze i zbliża się do zera. Mówimy, że granica tego ciągu wynosi 0.
• Ciąg rozbieżny: $a_n = n$. Wyrazy to: $1, 2, 3, 4, \dots$. Ten ciąg rośnie nieograniczenie i zmierza do nieskończoności. Nie zbliża się do żadnej konkretnej liczby, więc mówimy, że jest rozbieżny do nieskończoności.
• Ciąg rozbieżny: $a_n = (-1)^n$. Wyrazy to: $-1, 1, -1, 1, \dots$. Ten ciąg oscyluje między $-1$ a $1$ i nigdy nie zbliża się do jednej konkretnej wartości. Dlatego mówimy, że ten ciąg nie ma granicy.

Twierdzenie o trzech ciągach (twierdzenie o ściskaniu) jest niezwykle użytecznym narzędziem, szczególnie gdy mamy do czynienia z granicami ciągów zawierających funkcje trygonometryczne, takie jak sinus czy cosinus. Mówi ono, że jeśli mamy trzy ciągi $(a_n)$, $(b_n)$ i $(c_n)$ takie, że od pewnego miejsca $a_n \le b_n \le c_n$ dla każdego $n$, oraz granice ciągów $(a_n)$ i $(c_n)$ są równe pewnej liczbie $g$ (czyli $\lim_{n \to \infty} a_n = g$ i $\lim_{n \to \infty} c_n = g$), to ciąg $(b_n)$ również musi mieć tę samą granicę $g$. Na przykład, jeśli chcemy obliczyć granicę ciągu $b_n = \frac{\sin n}{n}$, wiemy, że $-1 \le \sin n \le 1$. Dzieląc przez $n$ (dla $n>0$), otrzymujemy $-\frac{1}{n} \le \frac{\sin n}{n} \le \frac{1}{n}$. Ponieważ granice ciągów $-\frac{1}{n}$ i $\frac{1}{n}$ wynoszą 0, to na mocy twierdzenia o trzech ciągach, granica $\frac{\sin n}{n}$ również wynosi 0.

Granica funkcji: Kiedy funkcja do czegoś dąży?

Podczas gdy granica ciągu dotyczy zachowania wartości wraz ze wzrostem indeksu $n$, granica funkcji analizuje, co dzieje się z wartościami funkcji $f(x)$, gdy jej argument $x$ zbliża się do pewnej ustalonej wartości $x_0$ (lub do nieskończoności). Chodzi o to, aby zrozumieć, do jakiej wartości "zbliża się" $f(x)$, gdy $x$ "zbliża się" do $x_0$. Co ważne, wartość funkcji w samym punkcie $x_0$ (czyli $f(x_0)$) nie musi istnieć ani nie musi być równa granicy.

Jednym ze sposobów na intuicyjne zrozumienie granicy funkcji jest definicja Heinego, która odwołuje się do granic ciągów. Mówi ona, że jeśli dla dowolnego ciągu argumentów $(x_n)$, który jest zbieżny do $x_0$ (i $x_n \neq x_0$), ciąg odpowiadających mu wartości funkcji $(f(x_n))$ jest zbieżny do $g$, to mówimy, że granica funkcji $f(x)$ w punkcie $x_0$ wynosi $g$. Jest to bardzo obrazowe jeśli niezależnie od tego, jakimi "ścieżkami" (ciągami argumentów) zbliżamy się do punktu $x_0$, wartości funkcji zawsze dążą do tej samej liczby $g$, to właśnie $g$ jest granicą funkcji w $x_0$.

Dla tych, którzy lubią bardziej formalne podejście, istnieje definicja Cauchy'ego (zwana też definicją $\epsilon$-$\delta$). Mówi ona, że funkcja $f(x)$ ma granicę $g$ w punkcie $x_0$, jeśli dla każdego, dowolnie małego, dodatniego $\epsilon$ (reprezentującego małą odległość wokół $g$), istnieje takie $\delta > 0$ (reprezentujące małą odległość wokół $x_0$), że dla wszystkich $x$ spełniających warunek $0 < |x - x_0| < \delta$, zachodzi nierówność $|f(x) - g| < \epsilon$. W skrócie: możemy sprawić, że wartości funkcji $f(x)$ będą dowolnie blisko $g$, po prostu wybierając $x$ wystarczająco blisko $x_0$ (ale nie równe $x_0$).

Czasami ważne jest, aby rozważyć, jak funkcja zachowuje się, gdy zbliżamy się do punktu $x_0$ tylko z jednej strony. Wprowadzamy wtedy pojęcie granic jednostronnych. Granica lewostronna oznacza, że zbliżamy się do $x_0$ od wartości mniejszych niż $x_0$ (oznaczamy jako $\lim_{x \to x_0^-} f(x)$), a granica prawostronna od wartości większych niż $x_0$ (oznaczamy jako $\lim_{x \to x_0^+} f(x)$). Kluczowa zasada mówi, że ogólna granica funkcji w punkcie $x_0$ istnieje wtedy i tylko wtedy, gdy istnieją obie granice jednostronne (lewostronna i prawostronna) i są one sobie równe. Na przykład, dla funkcji signum (sygnał), która wynosi $-1$ dla $x<0$, $0$ dla $x=0$ i $1$ dla $x>0$, granica lewostronna w punkcie 0 wynosi $-1$, prawostronna wynosi $1$. Ponieważ są różne, funkcja ta nie ma granicy w punkcie 0.

Co się dzieje, gdy wartości funkcji "uciekają" w nieskończoność, gdy argument zbliża się do pewnego punktu? Mówimy wtedy o granicach niewłaściwych. Na przykład, dla funkcji $f(x) = \frac{1}{x^2}$, gdy $x$ zbliża się do 0 (zarówno z lewej, jak i z prawej strony), wartości funkcji rosną nieograniczenie i dążą do $+\infty$. Takie zachowanie funkcji często wiąże się z istnieniem asymptoty pionowej prostej pionowej, do której funkcja się zbliża, ale nigdy jej nie dotyka. W tym przypadku, oś $y$ (prosta $x=0$) jest asymptotą pionową dla funkcji $\frac{1}{x^2}$.

Warsztat matematyka: Skuteczne metody obliczania granic

Teoretyczne definicje są ważne, ale w praktyce często musimy obliczyć konkretną wartość granicy. Na szczęście matematyka dostarcza nam zestaw sprawdzonych technik i narzędzi, które znacznie ułatwiają ten proces. Zrozumienie tych metod jest kluczem do skutecznego rozwiązywania zadań.

Podstawą obliczeń są arytmetyczne własności granic. Jeśli znamy granice dwóch funkcji (lub ciągów) i obie istnieją (są skończone), to możemy łatwo obliczyć granice ich sumy, różnicy, iloczynu, ilorazu oraz iloczynu przez stałą. Na przykład, granica sumy dwóch funkcji jest równa sumie ich granic. Te własności działają jak "klocki", z których budujemy bardziej złożone obliczenia.

Jednym z najczęstszych problemów, na które natrafiamy przy obliczaniu granic, są tzw. symbole nieoznaczone. Są to wyrażenia, które powstają podczas podstawienia granicznej wartości argumentu do wzoru funkcji, a które nie dają nam od razu odpowiedzi. Wynika to z faktu, że te same symbole mogą być granicą różnych funkcji, prowadząc do różnych wyników. Najczęściej spotykane symbole nieoznaczone to:

• $\frac{0}{0}$
• $\frac{\infty}{\infty}$
• $\infty - \infty$
• $0 \cdot \infty$
• $1^\infty$
• $\infty^0$
• $0^0$

Gdy napotkamy taki symbol, wiemy, że potrzebujemy dodatkowych technik, aby "ujawnić" właściwą granicę.

Dla symbolu nieoznaczonego $\frac{0}{0}$ w przypadku funkcji wymiernych (wielomianów), bardzo skuteczną metodą jest rozkład na czynniki. Polega on na takim przekształceniu licznika i mianownika, aby można było skrócić wspólny czynnik, który powoduje zerowanie się obu wyrażeń. Często wykorzystujemy do tego wzory skróconego mnożenia lub dzielenie wielomianów. Na przykład, aby obliczyć granicę $\lim_{x \to 2} \frac{x^2 - 4}{x - 2}$, po podstawieniu $x=2$ otrzymujemy $\frac{0}{0}$. Rozkładając licznik jako $(x-2)(x+2)$, możemy skrócić $(x-2)$ i otrzymać $\lim_{x \to 2} (x+2) = 4$.

Podobnie, dla symbolu nieoznaczonego $\frac{\infty}{\infty}$ (często pojawiającego się przy granicach w nieskończoności funkcji wymiernych), standardową techniką jest wyciągnięcie najwyższej potęgi $x$ przed nawias w liczniku i mianowniku. Na przykład, przy granicy $\lim_{x \to \infty} \frac{3x^2 + 2x}{x^2 + 1}$, wyciągamy $x^2$ z licznika i mianownika: $\lim_{x \to \infty} \frac{x^2(3 + 2/x)}{x^2(1 + 1/x^2)} = \lim_{x \to \infty} \frac{3 + 2/x}{1 + 1/x^2}$. Ponieważ $\frac{2}{x} \to 0$ i $\frac{1}{x^2} \to 0$ przy $x \to \infty$, granica wynosi $\frac{3+0}{1+0} = 3$.

Gdy w wyrażeniu pojawiają się pierwiastki, a obliczenia prowadzą do symboli nieoznaczonych takich jak $\frac{0}{0}$ lub $\infty - \infty$, często ratunkiem jest mnożenie przez sprzężenie. Sprzężenie wyrażenia $\sqrt{a} - \sqrt{b}$ to $\sqrt{a} + \sqrt{b}$ (i na odwrót). Mnożąc licznik i mianownik przez sprzężenie, możemy wykorzystać wzór $(a-b)(a+b) = a^2 - b^2$, co często pozwala pozbyć się pierwiastków w liczniku lub mianowniku i uprościć wyrażenie. Na przykład, przy granicy $\lim_{x \to 0} \frac{\sqrt{x+1} - 1}{x}$, po podstawieniu $x=0$ mamy $\frac{0}{0}$. Mnożąc licznik i mianownik przez sprzężenie $\sqrt{x+1} + 1$, otrzymujemy $\lim_{x \to 0} \frac{(\sqrt{x+1} - 1)(\sqrt{x+1} + 1)}{x(\sqrt{x+1} + 1)} = \lim_{x \to 0} \frac{(x+1) - 1}{x(\sqrt{x+1} + 1)} = \lim_{x \to 0} \frac{x}{x(\sqrt{x+1} + 1)} = \lim_{x \to 0} \frac{1}{\sqrt{x+1} + 1} = \frac{1}{\sqrt{0+1} + 1} = \frac{1}{2}$.

Reguła de L'Hôpitala to potężne narzędzie, które jest szczególnie przydatne na studiach. Można jej użyć, gdy mamy do czynienia z symbolami nieoznaczonymi $\frac{0}{0}$ lub $\frac{\infty}{\infty}$. Warunkiem jej zastosowania jest, aby funkcje w liczniku i mianowniku były różniczkowalne w pewnym otoczeniu punktu, do którego dążymy (lub w nieskończoności), a pochodna mianownika była różna od zera. Reguła mówi, że granica ilorazu funkcji jest równa granicy ilorazu ich pochodnych: $\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}$, pod warunkiem, że ta druga granica istnieje. Jest to bardzo wygodna metoda, pozwalająca uniknąć żmudnych przekształceń algebraicznych, choć wymaga znajomości pochodnych.

Granica a ciągłość funkcji: Nierozerwalny związek

Pojęcie granicy jest nie tylko narzędziem do obliczeń, ale także fundamentem do zrozumienia, czy funkcja jest "dobrze zachowana", czyli czy jest ciągła. Ciągłość funkcji oznacza, że jej wykres można narysować "jednym pociągnięciem ołówka", bez podnoszenia go z kartki nie ma żadnych przerw, skoków ani dziur. Granice pozwalają nam precyzyjnie zdefiniować, co to znaczy "bez przerw".

Funkcja $f(x)$ jest ciągła w punkcie $x_0$ wtedy i tylko wtedy, gdy spełnione są trzy warunki:

1. Wartość funkcji w punkcie $x_0$ istnieje, czyli $f(x_0)$ jest określone.
2. Granica funkcji $f(x)$ w punkcie $x_0$ istnieje (czyli granica lewostronna równa się prawostronnej).
3. Granica funkcji w punkcie $x_0$ jest równa wartości funkcji w tym punkcie, czyli $\lim_{x \to x_0} f(x) = f(x_0)$.

Jeśli którykolwiek z tych warunków nie jest spełniony, funkcja jest nieciągła w punkcie $x_0$. Intuicyjnie, oznacza to, że gdy zbliżamy się do punktu $x_0$, wartość funkcji zbliża się do tej samej liczby, którą funkcja przyjmuje w samym punkcie $x_0$.

Aby zbadać ciągłość funkcji w danym punkcie $x_0$, należy wykonać następujące kroki:

1. Oblicz wartość funkcji w punkcie $x_0$: Sprawdź, czy $f(x_0)$ jest zdefiniowane. Jeśli nie, funkcja jest na pewno nieciągła w tym punkcie.
2. Oblicz granicę funkcji w punkcie $x_0$: Użyj odpowiednich metod (algebraicznych, de L'Hôpitala itp.), aby znaleźć $\lim_{x \to x_0} f(x)$. Jeśli granica nie istnieje, funkcja jest nieciągła.
3. Porównaj wartość granicy z wartością funkcji: Jeśli obie istnieją i są sobie równe, funkcja jest ciągła w $x_0$. W przeciwnym razie jest nieciągła.

Zastosowania granic: Drzwi do wyższej matematyki

Granice to nie tylko abstrakcyjne konstrukcje matematyczne, ale potężne narzędzia, które otwierają drzwi do głębszego zrozumienia matematyki i jej zastosowań w świecie rzeczywistym. Są one fundamentem dla dwóch kluczowych działów analizy matematycznej: rachunku różniczkowego i całkowego.

Od granicy do pochodnej: fundament rachunku różniczkowego. Pochodna funkcji w danym punkcie opisuje chwilowe tempo zmian tej funkcji, czyli jej nachylenie w tym punkcie. Definicja pochodnej jest ściśle związana z granicą. Jest to granica ilorazu różnicowego: $f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}$. Analizując, do czego dąży ten iloraz, gdy $h$ staje się nieskończenie małe, możemy precyzyjnie określić tempo zmian funkcji w danym punkcie. To właśnie pochodne pozwalają nam opisywać prędkość, przyspieszenie, szybkość reakcji chemicznych i wiele innych dynamicznych procesów.

Jak granice pomagają obliczać pola powierzchni, czyli wstęp do całek. Całka oznaczona funkcji na danym przedziale geometrycznie reprezentuje pole powierzchni pod wykresem tej funkcji. Aby ją zdefiniować, również korzystamy z pojęcia granicy. Dzielimy przedział na wiele małych podprzedziałów i sumujemy pola prostokątów (lub innych prostych figur) opartych na wartościach funkcji w tych podprzedziałach. Gdy liczba podprzedziałów dąży do nieskończoności (a szerokość każdego z nich do zera), suma tych pól zbiega do dokładnej wartości całki. Jest to tzw. suma Riemanna, której granicę obliczamy, aby znaleźć pole pod krzywą, co ma zastosowanie w obliczaniu objętości, pracy, przepływu i wielu innych wielkości fizycznych.

Przeczytaj również: Jak rozwiązywać równania kwadratowe - proste metody i przykłady

Twoja droga do zrozumienia granic: kluczowe wnioski i kolejne kroki

Mam nadzieję, że ta podróż przez świat granic była dla Ciebie owocna. Dotarliśmy do sedna tego fundamentalnego pojęcia matematycznego, wyjaśniając jego intuicyjne znaczenie, formalne definicje, praktyczne metody obliczeniowe oraz kluczowe zastosowania w analizie matematycznej. Teraz wiesz już, dlaczego granice są tak ważne i jak sobie z nimi radzić.

• Granica opisuje zachowanie funkcji lub ciągu, gdy argumenty zbliżają się do określonej wartości lub nieskończoności.
• Zrozumienie granic jest niezbędne do pojęcia pochodnych i całek, kluczowych w wyższej matematyce i naukach ścisłych.
• Techniki takie jak rozkład na czynniki, mnożenie przez sprzężenie i reguła de L'Hôpitala są kluczowe w obliczaniu granic, zwłaszcza przy symbolach nieoznaczonych.
• Ciągłość funkcji jest ściśle związana z istnieniem i wartością jej granicy w danym punkcie.

Z mojego doświadczenia wynika, że najtrudniejszy jest często pierwszy krok przełamanie bariery abstrakcji. Jednak pamiętaj, że każde, nawet najmniejsze, zadanie rozwiązane samodzielnie, buduje Twoją pewność siebie i pogłębia zrozumienie. Nie zniechęcaj się, jeśli na początku coś wydaje się skomplikowane. Matematyka wymaga cierpliwości i systematyczności, a granice są tego doskonałym przykładem. Z czasem zobaczysz, jak wiele drzwi otwiera przed Tobą ta wiedza.

A jakie są Twoje dotychczasowe doświadczenia z granicami? Która z omówionych metod wydaje Ci się najbardziej pomocna w rozwiązywaniu zadań? Podziel się swoją opinią w komentarzach!