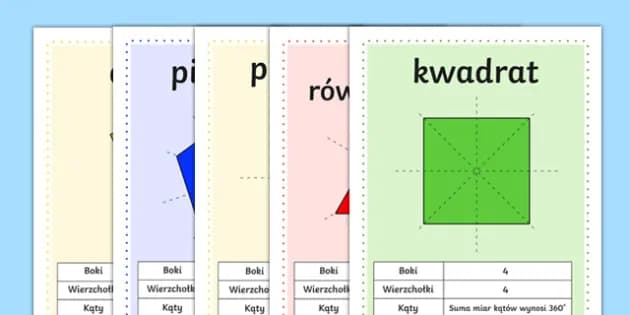
Figury geometryczne to podstawowe kształty w geometrii. Dzielą się na płaskie i przestrzenne. Do płaskich należą punkty, linie i wielokąty. Przestrzenne to bryły jak sześcian czy kula. Każda figura ma swoje unikalne właściwości, takie jak długość boków, kąty, pole powierzchni lub objętość.
Znajomość figur geometrycznych jest kluczowa w matematyce. Pozwala zrozumieć otaczający nas świat i rozwiązywać praktyczne problemy. Od prostych trójkątów po skomplikowane bryły, geometria jest wszędzie wokół nas.
Najważniejsze informacje:- Figury dzielą się na płaskie i przestrzenne
- Podstawowe figury płaskie to punkt, prosta, półprosta i odcinek
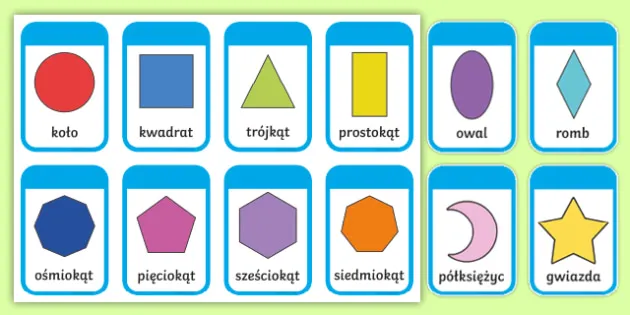
- Wielokąty mają różną liczbę boków, np. trójkąt, kwadrat, pięciokąt
- Koło i okrąg to figury okrągłe
- Bryły to figury trójwymiarowe, np. sześcian, prostopadłościan, kula
- Każda figura ma swoje charakterystyczne właściwości i wzory
Figury geometryczne - definicja i podstawowe pojęcia
Figury geometryczne to podstawowe kształty badane w geometrii. Reprezentują one abstrakcyjne formy obiektów występujących w rzeczywistości.
Znajomość rodzajów figur geometrycznych pozwala nam lepiej rozumieć i opisywać otaczający nas świat. Od prostych linii po skomplikowane bryły, geometria jest wszechobecna w naszym życiu.
- Punkt - podstawowy element geometrii, nie ma wymiarów
- Prosta - linia bez początku i końca
- Odcinek - część prostej ograniczona dwoma punktami
- Kąt - figura utworzona przez dwie półproste o wspólnym początku
- Wielokąt - figura płaska ograniczona łamaną zamkniętą
Klasyfikacja figur płaskich w geometrii
Podstawowe figury geometryczne dzielą się na płaskie i przestrzenne. Figury płaskie to te, które można narysować na kartce papieru bez podnoszenia ołówka. Należą do nich punkty, linie, wielokąty i figury okrągłe.
Wielokąty to figury zamknięte, ograniczone odcinkami. Ich nazwa zależy od liczby boków - trójkąty mają trzy boki, czworokąty cztery, a pięciokąty pięć. Figury okrągłe, jak koło i okrąg, nie mają boków ani wierzchołków.
| Figura | Nazwa | Główne cechy |
|---|---|---|
| . | Punkt | Nie ma wymiarów |
| --- | Odcinek | Część prostej ograniczona dwoma punktami |
| △ | Trójkąt | Trzy boki, trzy kąty |
| □ | Kwadrat | Cztery równe boki, cztery kąty proste |
| ○ | Koło | Wszystkie punkty w równej odległości od środka |
| ⬠ | Pięciokąt | Pięć boków, pięć kątów |
Najważniejsze wielokąty i ich właściwości
Trójkąty są najprostszymi wielokątami, mającymi trzy boki i trzy kąty. Ich suma kątów wewnętrznych zawsze wynosi 180 stopni.
Czworokąty to figury o czterech bokach, wśród których wyróżniamy kwadraty, prostokąty, romby i trapezy. Suma ich kątów wewnętrznych wynosi 360 stopni.
Wielokąty o większej liczbie boków, takie jak pięciokąty czy sześciokąty, mają bardziej złożone właściwości. Ich suma kątów wewnętrznych rośnie wraz z liczbą boków.
Trójkąty - rodzaje i charakterystyka
Trójkąty klasyfikujemy ze względu na długość boków i miary kątów. Możemy mieć trójkąty równoboczne, równoramienne i różnoboczne, a także ostrokątne, prostokątne i rozwartokątne.
Każdy typ trójkąta ma unikalne cechy. Na przykład, trójkąt równoboczny ma wszystkie boki i kąty równe, a trójkąt prostokątny zawiera jeden kąt prosty.
- Trójkąt równoboczny: wszystkie boki i kąty równe (60°)
- Trójkąt prostokątny: jeden kąt prosty (90°)
- Trójkąt równoramienny: dwa boki równej długości
Czworokąty w życiu codziennym
Czworokąty są wszechobecne w naszym otoczeniu. Kwadraty i prostokąty widzimy w oknach, drzwiach i ekranach urządzeń elektronicznych.
Romby często pojawiają się w biżuterii i znakach drogowych, podczas gdy trapezy można znaleźć w architekturze i designie mebli. Czworokąty są również podstawą wielu logo firm i marek.
Spójrz wokół siebie - zauważysz czworokąty w kształcie książek, stołów czy smartfonów. Te kształty geometryczne są fundamentem naszego codziennego życia.
Bryły geometryczne i ich zastosowanie
Bryły to trójwymiarowe figury geometryczne. Najprostsze z nich to sześcian, prostopadłościan i kula.
W życiu codziennym bryły geometryczne spotykamy na każdym kroku. Pudełka, budynki, piłki - wszystko to przykłady brył.
Znajomość właściwości brył jest kluczowa w architekturze, inżynierii i projektowaniu. Pozwala na tworzenie stabilnych konstrukcji i funkcjonalnych przedmiotów.
| Bryła | Cechy | Przykład z życia |
|---|---|---|
| Sześcian | 6 kwadratowych ścian | Kostka do gry |
| Prostopadłościan | 6 prostokątnych ścian | Pudełko |
| Kula | Nieskończenie wiele punktów równo oddalonych od środka | Piłka |
| Walec | Dwie równoległe podstawy kołowe | Puszka |
| Stożek | Okrągła podstawa i wierzchołek | Rożek lodowy |
Jak obliczyć pole i obwód figur?
Obliczanie pola i obwodu figur geometrycznych jest kluczowe w wielu dziedzinach. Pozwala na precyzyjne planowanie przestrzeni i materiałów.
Dla każdej figury istnieją specyficzne wzory. Znajomość tych formuł umożliwia rozwiązywanie praktycznych problemów, od malowania ścian po projektowanie ogrodów.
Umiejętność szybkiego szacowania wymiarów jest przydatna w codziennym życiu. Oto kilka podstawowych wzorów:
- Pole kwadratu: a²
- Pole prostokąta: a × b
- Pole trójkąta: (a × h) / 2
Wzory na objętość podstawowych brył
Obliczanie objętości brył jest istotne w wielu praktycznych zastosowaniach. Od określania pojemności zbiorników po projektowanie opakowań, te obliczenia są niezbędne.
Każda bryła ma swój charakterystyczny wzór na objętość. Znajomość tych formuł pozwala na efektywne rozwiązywanie problemów przestrzennych.
Przykład 1: Oblicz objętość sześcianu o boku 5 cm.
Rozwiązanie: V = a³ = 5³ = 125 cm³
Przykład 2: Jaką objętość ma walec o promieniu podstawy 3 cm i wysokości 10 cm?
Rozwiązanie: V = πr²h = π × 3² × 10 ≈ 282,74 cm³
Figury geometryczne: klucz do zrozumienia świata wokół nas
Figury geometryczne to fundamentalne elementy kształtujące nasze otoczenie. Od prostych punktów i linii, przez wielokąty, aż po skomplikowane bryły - geometria jest wszechobecna w naszym życiu codziennym.
Poznanie podstawowych figur geometrycznych i ich właściwości otwiera drzwi do lepszego zrozumienia architektury, designu czy inżynierii. Umiejętność rozpoznawania i obliczania pól, obwodów czy objętości figur ma praktyczne zastosowanie w wielu dziedzinach - od projektowania wnętrz po konstruowanie budynków.
Pamiętajmy, że kształty geometryczne to nie tylko abstrakcyjne pojęcia z podręczników matematyki. To narzędzia, które pozwalają nam opisywać i kształtować rzeczywistość. Czy to trójkąt w znaku drogowym, prostokątny ekran smartfona, czy sferyczna piłka - geometria jest integralną częścią naszego codziennego życia.
