Proporcje to jedno z tych matematycznych narzędzi, które w niezwykły sposób łączą abstrakcyjny świat liczb z konkretnymi sytuacjami z naszego życia. Niezależnie od tego, czy przygotowujesz obiad dla większej liczby gości, planujesz podróż, czy po prostu chcesz zrozumieć, jak działają zniżki, proporcje przychodzą z pomocą. Opanowanie ich znaczenia i sposobu użycia to klucz do łatwiejszego radzenia sobie z wieloma problemami, nie tylko szkolnymi.
Proporcje w matematyce klucz do zrozumienia zależności w świecie liczb i życia codziennego
- Proporcje to fundamentalne zagadnienie matematyczne, wprowadzane w szkole podstawowej, opisujące zależności między wielkościami.
- Wyróżniamy proporcjonalność prostą (wzrost jednej wartości powoduje wzrost drugiej) i odwrotną (wzrost jednej wartości powoduje spadek drugiej).
- Kluczową metodą rozwiązywania zadań z proporcjonalnością prostą jest "metoda na krzyż".
- Proporcje mają szerokie zastosowanie w życiu codziennym, m.in. w gotowaniu, przeliczaniu walut, skali map czy chemii.
- Najczęstsze błędy to mylenie proporcjonalności prostej z odwrotną oraz nieprawidłowe ułożenie danych w równaniu.
Definicja proporcji: odkoduj matematyczny żargon
W najprostszych słowach, proporcja to po prostu równość dwóch stosunków. Mówiąc jeszcze prościej, porównujemy, jak jedna para liczb ma się do siebie, i sprawdzamy, czy ta sama relacja zachodzi dla innej pary liczb. To fundamentalne zagadnienie w polskiej podstawie programowej matematyki, które pojawia się już w 6. klasie szkoły podstawowej i stanowi podstawę do zrozumienia wielu bardziej zaawansowanych zagadnień. Zrozumienie proporcji pozwala nam dostrzec i opisać zależności między różnymi wielkościami.
Wielkości wprost i odwrotnie proporcjonalne: klucz do zrozumienia problemu
Kiedy mówimy o proporcjach, najczęściej mamy na myśli dwa rodzaje zależności między wielkościami: prostą i odwrotną. Proporcjonalność prosta (wprost proporcjonalność) zachodzi wtedy, gdy dwie wielkości rosną lub maleją w tym samym tempie. Jeśli jedna wielkość zwiększy się dwa razy, druga również zwiększy się dwa razy. Przykładem może być zależność między liczbą kupionych jabłek a ich całkowitą ceną im więcej jabłek kupisz, tym więcej zapłacisz. Matematycznie możemy to zapisać jako y = a*x, gdzie 'a' to stały współczynnik proporcjonalności.
Z kolei proporcjonalność odwrotna to sytuacja, w której wzrost jednej wielkości powoduje proporcjonalny spadek drugiej. Jeśli jedna wielkość zwiększy się dwa razy, druga zmniejszy się dwa razy. Klasycznym przykładem jest zależność między prędkością pojazdu a czasem potrzebnym na pokonanie ustalonego dystansu. Im szybciej jedziesz, tym krócej trwa podróż. Wzór opisujący tę zależność to y = a/x, gdzie 'a' jest stałym współczynnikiem.
Proporcje poza szkołą: od gotowania po planowanie podróży
Proporcje to nie tylko szkolne zadania. Są one wszechobecne w naszym codziennym życiu:
- Przeliczanie jednostek: Czy to walut obcych, czy miar (np. z kilogramów na funty), proporcje pomagają nam dokonać precyzyjnych zamian.
- Gotowanie: Zwiększasz porcję obiadu dla gości? Musisz proporcjonalnie zwiększyć ilość wszystkich składników, aby zachować smak i konsystencję potrawy.
- Skala na mapach: Odległość na mapie jest zawsze proporcjonalna do rzeczywistej odległości na ziemi, co pozwala nam planować trasy i oceniać dystanse.
- Prędkość, czas i dystans: Obliczanie, ile czasu zajmie nam dojazd do celu przy danej prędkości, to klasyczny przykład proporcjonalności odwrotnej.
- Zużycie paliwa: Wiedząc, ile paliwa zużywa samochód na 100 km, możemy obliczyć, ile paliwa potrzebujemy na dłuższą trasę.
- Wydajność pracy: Jeśli wiemy, ile czasu zajmuje jednej osobie wykonanie zadania, możemy oszacować, ile czasu zajmie to grupie osób.
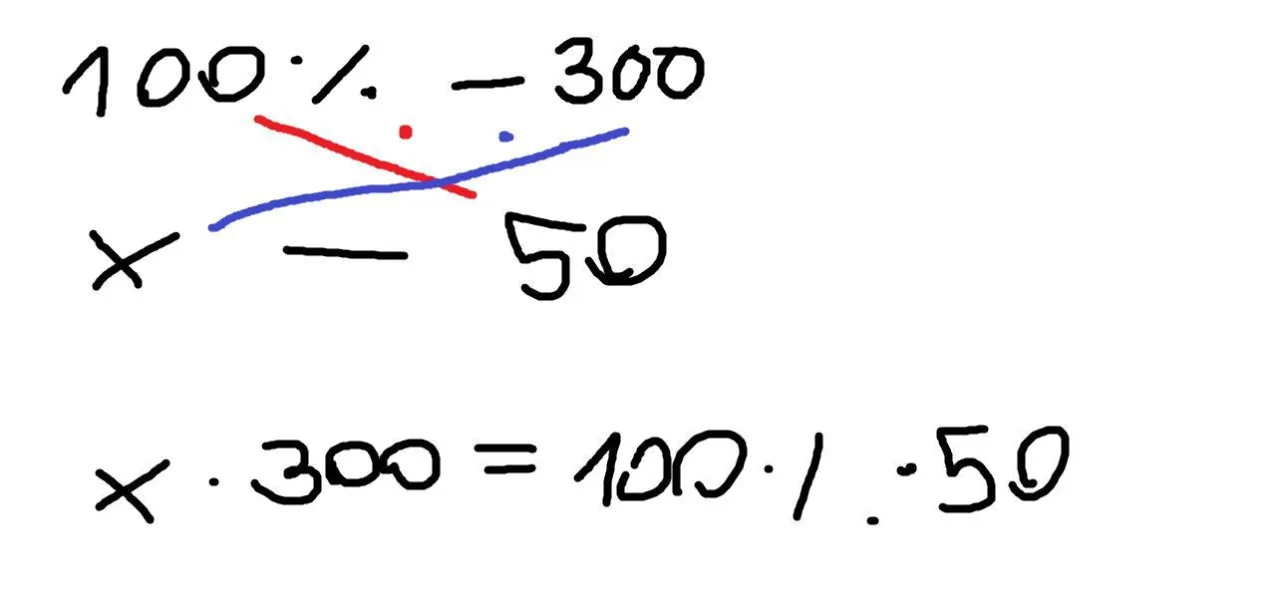
Proporcjonalność prosta: opanuj metodę "na krzyż" bez trudu
Kiedy dwie wartości rosną razem? Identyfikacja proporcjonalności prostej
Rozpoznanie proporcjonalności prostej polega na logicznym zastanowieniu się nad zależnością między wielkościami. Jeśli zauważamy, że wzrost jednej z nich nieuchronnie prowadzi do proporcjonalnego wzrostu drugiej, mamy do czynienia właśnie z tym typem zależności. Na przykład, jeśli cena jednej czekolady wynosi 3 zł, to cena dwóch czekolad będzie wynosić 6 zł, a trzech czekolad 9 zł. W tym przypadku cena rośnie dokładnie w tym samym tempie, co liczba kupionych czekolad.
Rozwiązywanie zadań krok po kroku: sprawdzony schemat działania
Najskuteczniejszą i najczęściej stosowaną metodą rozwiązywania zadań z proporcjonalności prostej jest tzw. "metoda na krzyż". Oto jak to działa:
- Dokładnie przeczytaj zadanie: Zrozum, jakie wielkości są ze sobą powiązane i czego szukasz.
- Zidentyfikuj, czy to proporcjonalność prosta: Zastanów się, czy gdy jedna wielkość rośnie, druga też rośnie (lub gdy jedna maleje, druga też maleje).
- Ułóż dane w tabeli lub schematycznie: Wypisz znane pary wartości, pamiętając o tym, aby odpowiadające sobie wielkości znajdowały się w tej samej kolumnie lub wierszu.
- Oznacz niewiadomą: Wprowadź literę (np. 'x') dla szukanej wartości.
- Ułóż proporcję: Zapisz równanie, mnożąc "na krzyż" licznik pierwszej liczby przez mianownik drugiej i przyrównując to do iloczynu mianownika pierwszej liczby i licznika drugiej.
- Rozwiąż równanie: Wyznacz niewiadomą 'x'.
- Sprawdź wynik: Upewnij się, że otrzymana odpowiedź ma sens w kontekście zadania.
Przykład: Jeśli 3 kg jabłek kosztuje 12 zł, to ile kosztuje 5 kg tych samych jabłek?
Zakładamy proporcjonalność prostą: więcej kilogramów to więcej złotówek.
Układamy proporcję:
3 kg ---- 12 zł
5 kg ---- x zł
Metoda na krzyż: 3 * x = 5 * 12
3x = 60
x = 60 / 3
x = 20 zł
Zatem 5 kg jabłek kosztuje 20 zł.
Praktyczne przykłady: zakupy, przepisy kulinarne i przeliczanie walut
Załóżmy, że chcemy kupić 4 batony, które kosztują 2 złote za sztukę. Ile zapłacimy? Układamy proporcję: 1 baton to 2 zł, więc 4 batony to x zł. 1/2 = 4/x, co daje x = 8 zł. Proste, prawda?
Twoja ulubiona babcina receptura na ciasto wymaga 200g mąki na 4 porcje. Chcesz przygotować ciasto dla 10 porcji. Ile mąki potrzebujesz? Proporcja: 200g na 4 porcje, x g na 10 porcji. 200/4 = x/10, co daje x = 500g mąki.
Jesteś na wakacjach i 1 euro kosztuje 4,50 zł. Chcesz wymienić 100 euro. Ile złotówek otrzymasz? Proporcja: 1 euro to 4,50 zł, więc 100 euro to x zł. 1/4.50 = 100/x, co daje x = 450 zł.
Proporcjonalność odwrotna: gdy jedna wartość rośnie, a druga maleje
Rozpoznawanie zależności odwrotnej: prędkość, czas i wydajność pracy
Proporcjonalność odwrotną rozpoznajemy, gdy widzimy, że jedna wielkość działa "przeciwko" drugiej. Na przykład, jeśli samochód jedzie z prędkością 50 km/h i pokonuje trasę w 2 godziny, to jadąc z prędkością 100 km/h (czyli dwa razy szybciej), pokona tę samą trasę w 1 godzinę (czyli dwa razy krócej). Inny przykład to wydajność pracy: jeśli 4 pracowników maluje płot w 6 godzin, to 8 pracowników (dwa razy więcej) pomaluje ten sam płot w 3 godziny (dwa razy krócej). Zawsze warto zadać sobie pytanie: "Czy gdy jedna rzecz się zwiększa, druga musi się zmniejszyć, aby zachować pewną stałą relację?".
Jak poprawnie ułożyć równanie? Uniknij typowych pułapek
Układanie równania dla proporcjonalności odwrotnej wymaga nieco innej logiki niż w przypadku proporcjonalności prostej. Zamiast mnożyć "na krzyż", musimy pamiętać, że iloczyn odpowiadających sobie wielkości jest stały. Jeśli mamy zależność, że 2 robotników wykonuje zadanie w 12 godzin, to iloczyn wynosi 2 * 12 = 24 (roboczogodziny). Jeśli teraz chcemy wiedzieć, ile czasu zajmie to 4 robotnikom, układamy równanie: 4 * x = 24, gdzie 'x' to szukany czas. Rozwiązanie to x = 24 / 4 = 6 godzin. Kluczem jest tutaj utrzymanie stałego iloczynu.
Zadania z życia wzięte: od malowania ścian po podział zapasów
Załóżmy, że 3 malarzy potrafi pomalować pokój w 8 godzin. Ile czasu zajmie to 4 malarzom? Zakładamy proporcjonalność odwrotną: więcej malarzy, krótszy czas. Iloczyn: 3 * 8 = 24 roboczogodziny. Dla 4 malarzy: 4 * x = 24, czyli x = 6 godzin.
Masz zapas 120 kg karmy dla psa, który wystarcza na 30 dni. Jeśli przygarniesz drugiego psa (czyli będziesz miał łącznie 2 psy), na ile dni wystarczy ta sama ilość karmy? Proporcjonalność odwrotna: więcej psów, krótszy czas. Iloczyn: 1 * 30 = 30 dni*psa. Dla 2 psów: 2 * x = 30, czyli x = 15 dni.
Jak odróżnić proporcjonalność prostą od odwrotnej? Niezawodny test
Zadaj sobie kluczowe pytanie: "Co się stanie z drugą wartością, gdy pierwsza wzrośnie?"
To jest absolutnie najważniejszy krok w rozwiązywaniu zadań z proporcjami. Zanim zaczniesz cokolwiek liczyć, zadaj sobie proste pytanie: "Jeśli pierwsza wielkość (np. liczba kupionych produktów) się zwiększy, to czy druga wielkość (np. cena) też się zwiększy, czy zmaleje?". Jeśli obie rosną lub obie maleją to proporcjonalność prosta. Jeśli jedna rośnie, a druga maleje to proporcjonalność odwrotna. Ten logiczny test jest niezawodny i pozwala uniknąć wielu błędów.
Analiza słów-kluczy w zadaniach tekstowych: na co zwrócić uwagę?
Czasami same sformułowania w zadaniu podpowiadają nam, z jakim typem proporcjonalności mamy do czynienia:
- Sugerujące proporcjonalność prostą: "im więcej..., tym więcej...", "za każdą sztukę...", "cena jednostkowa...", "współczynnik...", "każdego dnia..."
- Sugerujące proporcjonalność odwrotną: "im więcej osób..., tym mniej czasu...", "przy stałej prędkości...", "podzielić równo...", "wydajność pracy...", "wspólne wykonanie zadania..."
Zwracaj uwagę na te zwroty, a będą one dla Ciebie cenną wskazówką.
Tabela jako narzędzie: wizualizacja danych, która ułatwia myślenie
Prosta tabela może być nieocenioną pomocą w uporządkowaniu informacji i podjęciu właściwej decyzji. Wystarczy stworzyć tabelę z dwiema kolumnami (lub wierszami), gdzie w pierwszej kolumnie umieścimy jedną wielkość, a w drugiej odpowiadającą jej wielkość. Następnie wpisujemy znane pary danych, a dla szukanej wartości zostawiamy miejsce na niewiadomą. Wizualizacja danych w ten sposób często pozwala intuicyjnie dostrzec, czy zależności są proste, czy odwrotne.
Przykładowa struktura tabeli dla proporcjonalności prostej:
| Liczba sztuk | Cena (zł) |
|---|---|
| 3 | 12 |
| 5 | x |
A dla proporcjonalności odwrotnej:
| Liczba malarzy | Czas (godziny) |
|---|---|
| 3 | 8 |
| 4 | x |
Zaskakujące zastosowania proporcji: od map po finanse
Skala na mapie: jak proporcje pomagają odczytać realne odległości?
Skala na mapie, często zapisywana jako np. 1:100 000, to nic innego jak proporcja. Oznacza ona, że jeden centymetr na mapie odpowiada 100 000 centymetrów w rzeczywistości. Aby obliczyć rzeczywistą odległość, wystarczy zmierzyć odległość na mapie i pomnożyć ją przez wartość skali. Na przykład, jeśli na mapie odległość między dwoma miastami wynosi 5 cm, a skala to 1:100 000, to rzeczywista odległość wynosi 5 cm * 100 000 = 500 000 cm, czyli 5 km. To prosty przykład, jak proporcje pomagają nam nawigować w świecie.
Stężenia procentowe: niezbędne narzędzie chemika (i nie tylko)
W chemii, obliczanie stężeń procentowych roztworów jest kluczowe dla bezpieczeństwa i skuteczności eksperymentów. Proporcje są tutaj podstawowym narzędziem. Na przykład, jeśli chcemy przygotować 10% roztwór soli, a mamy 200g wody, musimy obliczyć, ile soli (x) potrzebujemy dodać, aby uzyskać pożądane stężenie. Proporcja wyglądałaby tak: 10% (czyli 10g soli na 100g roztworu) do x gramów soli na (200g wody + x gramów soli) całkowitej masy roztworu. To pokazuje, jak proporcje pozwalają nam precyzyjnie operować stężeniami.
Procent składany a proporcje: jak rosną Twoje oszczędności?
Choć procent składany może brzmieć skomplikowanie, jego podstawą są właśnie proporcje. Kiedy pieniądze "pracują" na lokacie, każdego okresu naliczane są odsetki od kwoty kapitału wraz z już naliczonymi odsetkami. To oznacza, że każdorazowo stosujemy proporcję do obliczenia odsetek od coraz większej kwoty. W ten sposób nasze oszczędności rosną w coraz szybszym tempie, co jest potężnym dowodem na siłę proporcjonalności w finansach.
Unikaj typowych błędów w zadaniach z proporcji
Błąd 1: Mylenie proporcjonalności prostej z odwrotną
To zdecydowanie najczęstsza pułapka, w którą wpadają uczniowie. Zanim zaczniesz rozwiązywać zadanie, poświęć chwilę na analizę zależności między wielkościami. Zawsze zadaj sobie pytanie: "Co się stanie z drugą wielkością, gdy pierwsza wzrośnie?". Jeśli odpowiedź nie jest oczywista, wróć do definicji i przykładów proporcjonalności prostej i odwrotnej. Prawidłowe rozpoznanie typu zależności to już połowa sukcesu.
Błąd 2: Nieprawidłowe ułożenie danych w równaniu
Nawet jeśli poprawnie zidentyfikujesz typ proporcjonalności, błąd w ułożeniu proporcji może prowadzić do całkowicie błędnej odpowiedzi. Pamiętaj o zasadzie: odpowiadające sobie wielkości muszą być w tej samej linii (w przypadku proporcjonalności prostej przy mnożeniu "na krzyż") lub ich iloczyn musi być stały (w przypadku proporcjonalności odwrotnej). Na przykład, jeśli 3 kg kosztuje 12 zł, to 5 kg nie może być w tej samej kolumnie co 12 zł, jeśli 3 kg jest w kolumnie z ceną. Poprawne ułożenie to klucz do sukcesu.
Błąd 3: Zapominanie o spójności jednostek
To subtelny, ale bardzo częsty błąd. Jeśli w zadaniu pojawiają się różne jednostki (np. cena podana w złotówkach za kilogram, a pytanie dotyczy ceny za gram; lub czas podany w godzinach i minutach), musisz je ujednolicić przed rozpoczęciem obliczeń. Na przykład, jeśli masz przeliczyć 2 godziny i 30 minut na minuty, musisz pamiętać, że 2 godziny to 120 minut, więc łącznie daje to 150 minut. Brak spójności jednostek niemal gwarantuje błędny wynik, nawet jeśli cała reszta obliczeń jest poprawna.
Przeczytaj również: Co oznacza w matematyce? Zrozum znaczenie symboli i notacji
Co warto zapamiętać? Kluczowe wnioski i Twoje następne kroki
Mam nadzieję, że ten artykuł pomógł Ci rozwiać wszelkie wątpliwości dotyczące proporcji. Teraz już wiesz, że proporcje to nie tylko abstrakcyjne wzory, ale potężne narzędzie do rozumienia świata wokół nas od kuchni po finanse. Opanowałeś definicje, nauczyłeś się odróżniać zależności proste od odwrotnych i poznałeś skuteczne metody ich rozwiązywania.
- Proporcje to równość dwóch stosunków, kluczowe do opisu zależności między wielkościami.
- Rozróżniaj proporcjonalność prostą (obie wielkości rosną/maleją razem) od odwrotnej (jedna rośnie, druga maleje).
- Metoda "na krzyż" jest niezawodna przy proporcjonalności prostej, a stały iloczyn przy proporcjonalności odwrotnej.
- Zawsze analizuj zadanie, zadając sobie pytanie o wzajemny wpływ wielkości, aby uniknąć błędów.
Z mojego doświadczenia wynika, że najwięcej problemów sprawia początkowa identyfikacja rodzaju proporcjonalności. Dlatego zachęcam Cię, abyś po przeczytaniu tego artykułu spróbował rozwiązać kilka prostych zadań, skupiając się właśnie na tym pierwszym kroku logicznej analizie zależności. To właśnie świadome podejście do problemu, a nie tylko mechaniczne stosowanie wzorów, buduje prawdziwe zrozumienie i pewność siebie w matematyce.
A jakie są Twoje doświadczenia z rozwiązywaniem zadań z proporcji? Czy któraś z metod okazała się dla Ciebie szczególnie pomocna? Podziel się swoją opinią w komentarzach!

